Ультразвуковые приборы, использующие время-импульсный метод, распространены очень широко. Основная погрешность измерения таких приборов обусловлена неточностью определения прихода ультразвукового импульса. Обычно момент прихода ультразвукового импульса определяют с помощью компаратора, но за счёт сложной формы ультразвукового импульса, время срабатывания компаратора не совпадает с началом импульса.
Если амплитуда и форма сигнала остаются постоянными, то погрешность определения времени распространения сигнала в среде остается постоянной и ее можно учесть. Однако на практике в процессе распространения сигнала уменьшается его амплитуда за счет расхождения и потерь в среде. Системы автоматической регулировки усиления позволяют поддерживать амплитуду сигнала постоянной. Но если в процессе распространения сигнала меняется его форма, что особенно сильно проявляется при распространении в ограниченных средах, то применение АРУ или компаратора со «следящим» порогом в этой ситуации не решают проблемы точности определения момента прихода импульса. Фундаментальной основой данного явления служит неравенство фазовых скоростей различных мод. Поэтому в процессе распространения импульса в ограниченных средах происходит «растягивание» сигнала во времени и изменение его формы.
Существенно повысить точность измерения можно, если применить современные методы обработки эхо-сигналов. Одним из таких методов [1] является метод аппроксимации огибающей эхо-сигнала кривой, описываемой полиномом второй степени:
![]() (1)
(1)
где s - амплитуда огибающей, t - время, a, b, c - коэффициенты полинома.
Так как форма эхо-импульса несимметрична относительно оси t, то для аппроксимации фронта используются две кривые. Одна кривая огибает импульс по положительным значениям, другая - по отрицательным значениям. Эти кривые имеют две общие точки, одна из которых принимается за начало исследуемого эхо-импульса.
Для нахождения коэффициентов a, b, c берутся значения амплитуды ультразвукового импульса в трёх точках, соответствующих вершинам (экстремумам) синусоидального сигнала в трёх соседних периодах. Используя эти данные, составляется система уравнений:
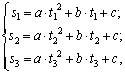 (2)
(2)
где s1, s2, s3 - значения амплитуды ультразвукового импульса в точках экстремумов в моменты времени t1, t2, t3.
Из системы уравнений (2) находятся коэффициенты a, b, c.
По такому же принципу можно аппроксимировать форму переднего фронта импульса кривой, описываемой полиномом третьей степени:
![]() (3)
(3)
Полином третьей степени в некоторых случаях аппроксимирует огибающую переднего фронта эхо-импульса с большей точностью, что даёт лучший результат. Для нахождения коэффициентов a, b, c, d составляется система из четырёх уравнений:
Решения систем уравнений (2) и (3) находятся с помощью метода Крамера [2]. Огибающие могут не пересекаться, поэтому в качестве начала эхо-импульса принимается точка наименьшего расстояния между огибающими.
В отличие от метода определения момента прихода эхо-импульса с помощью компаратора с фиксированным порогом срабатывания, погрешность методов огибающих второго и третьего порядков не зависит от амплитуды эхо-импульса, но зависит от его формы.
В реальных условиях на форму эхо-импульса существенно влияют помехи и шумы, которые приводят к ошибкам при расчёте уравнений огибающих. Чтобы уменьшить влияние помех и шумов на расчёт, для нахождения коэффициентов уравнения кривых был использован метод наименьших квадратов. Этот метод отличается тем, что в расчёт берётся количество точек, превышающее количество неизвестных переменных, и строится усреднённая огибающая по этим точкам. В общем случае метод наименьших квадратов используется для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки [3].
Коэффициенты аппроксимации находятся путём решения следующей системы уравнений:
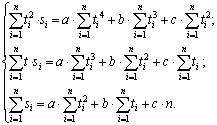
где n - количество точек экстремумов, выбранных для полиномиальной аппроксимации, индекс i - текущий номер экспериментальной точки.
В отличие от метода фиксации момента прихода сигнала с помощью компаратора с фиксированным порогом срабатывания, предлагаемый метод обеспечивает нулевую ошибку при любых линейных вариациях амплитуды сигнала. Это объясняется тем, что общий множитель всех элементов одного столбца (столбец значений, в которые входят величины si) может быть вынесен за знак определителя. Подстановка таких коэффициентов в выражения (2) и (3) не меняет результат его вычисления.
Анализ проведенных расчетов позволяет сделать вывод, что использование полинома третьей степени позволяет более точно описать огибающую эхо-импульса, особенно нарастающую его часть. Поэтому погрешность метода аппроксимации огибающей эхо-импульса полиномом третьего порядка составила 1/10 часть периода, а погрешность метода аппроксимации огибающей эхо-импульса полиномом второго порядка составила 1/2 часть периода.
Определим минимальную частоту дискретизации входного сигнала, обеспечивающую однозначное определение экстремумов в одном периоде входного сигнала. Для упрощения расчетов будем считать, что сигнал, поступающий на приемник, имеет синусоидальный вид с сохранением фазы, частоты и амплитуды в пределах одного периода. Максимальная ошибка в определении амплитудного значения напряжения будет в том случае, если два соседних отсчета АЦП с координатами (U1, ω⋅t1) и (U1, ω⋅t2) будут сделаны симметрично относительно экстремума, имеющего координаты (Um, π/2).
В этом случае фаза сигнала, при которой был сделан отсчет с координатами (U1, ω⋅t1) будет определяться из выражения:
![]()
где N - количество отсчетов АЦП за период.
Зная фазу можно найти амплитуду:
![]()
Абсолютная ошибка в определении амплитуды составит:
![]()
Отсюда находим относительную ошибку:
![]()
Если ошибка в определении максимальной амплитуды должна быть менее δ, то количество отсчетов определиться из выражения:
![]() (4)
(4)
Анализ выражения (4) позволяет сделать вывод, что при ошибке в определении амплитуды в 5 % количество отсчетов за период должно быть не менее 10, при 20 отсчетах - ошибка уменьшается до 1,5 %.
Для оценки точности рассматриваемого метода была получена экспериментальная зависимость погрешности измерения уровня от расстояния L между излучателем и приёмником. В эксперименте использовался круглый металлический волновод диаметром 52 мм. В качестве излучателя и приёмника использовались ультразвуковые преобразователи MA40B диаметром 16 мм. Они располагались по центру волновода. Частота ультразвуковых колебаний равна 40 кГц. По этим результатам можно сделать следующие выводы. Аппроксимация фронта эхо-импульса огибающей третьего порядка не даёт преимущества по сравнению с методом огибающей второго порядка, однако трудоемкость вычислений значительно выше. Поэтому, целесообразно применять метод огибающей второго порядка. Погрешность этого метода в основном определяется амплитудой эхо-импульса и правильным выбором расчётных точек. Применение метода аппроксимации нарастающей части эхо-импульса полиномом второй степени для определения времени прихода эхо-импульса позволяет в три раза повысить точность измерения ультразвуковых приборов, использующих время-импульсный метод. Однако для получения высоких метрологических характеристик необходимо обеспечить не менее 10 отсчетов за период. Поэтому область применения метода ограничивается частотами до 10 МГц.
Применение новых методов обработки эхо-импульсов позволяет существенно снизить погрешность измерения ультразвуковых приборов, использующих время-импульсный метод.
СПИСОК ЛИТЕРАТУРЫ
- Солдатов А.И., Цехановский С.А. Способ компенсации погрешности измерения ультразвукового уровнемера. Патент РФ №2358243, от 10.06.2009
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. - М., 1974. - 832 с.
- Андре Анго. Математика для электро- и радиоинженеров. - М.: Наука, 1965. - 779 с.



