В настоящей работе рассматриваются методы определения дисконтной функции, ставки спот и мгновенной форвардной ставки по ценам купонных облигаций, основанные на использовании сплайн-функций. Использовать сплайны для моделирования процентных ставок было предложено в работе [4] и затем этот подход применялся во многих работах. Здесь обсуждаются различные методы определения структуры процентных ставок по ценам купонных облигаций с помощью сплайн-функций.
Структура процентных ставок обычно представляется тремя кривыми: дисконтной функцией, ставкой спот (кривой доходности) и мгновенной форвардной ставкой [1].
Дисконтная функция 
описывает
текущую стоимость одного рубля, выплаченного через t лет. Для облигации с погашением в момент времени t ее текущая стоимость, характеризуемая текущей ценой
облигации B(t),
выражается
через дисконтную функция 8(t) при помощи формулы
где c - купонная ставка и F- номинал облигации.
Ставка спот (кривая
доходности) 
получается из дисконтной
функции следующим образом
Мгновенная форвардная
ставка 
представляет
ставку доходности на инвестиции, сделанные в бесконечно малый промежуток
времени 
. Мгновенная форвардная ставка связана с дисконтной
функцией следующим соотношением
Из этих определений ясно, что если одна из трех функций известна, другие две могут быть найдены. Определение мгновенной форвардной ставки подразумевает также, что дисконтная функция δ(t)
должна быть непрерывно дифференцируема, т.е. должна быть функцией класса С1.
Наиболее распространенным вариантом определения структуры процентных ставок с помощью сплайнов является построение с их помощью дисконтной функции.
Дисконтную
функцию представляют как линейную комбинацию n непрерывно дифференцируемых функций 
(например, B -сплайнов, экспоненциальных сплайнов): 
Носкольку стоимость 1 рубля в настоящий момент равна 1, необходимо,
чтобы δ(0) = 1. Поэтому a0 =
1 и fj(0)
= 0 . Таким образом, дисконтная функция приобретает вид 
Предположим, что модель для цены каждой облигации (плюс некоторый начисленный процент α) имеет вид
где e - нормально распределенная случайная величина с нулевым средним и дисперсией σ2 . В случае, если сплайны применяются к дисконтной функции,
где 
- n -мерный вектор,
составленный из набора
базисных функций 
- вектор моментов времени, в которые
производятся выплаты, y = B + α,
. Эта
спецификация удобна для оценивания параметров, поскольку дисконтная функция
линейна по отношению к неизвестным параметрам.
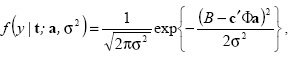
Однако сплайны можно применять не только напрямую к дисконтной функции, но и к доходности бескупонной облигации или к мгновенной форвардной ставке.
Предполагая, что сплайны применяются к доходности
бескупонной облигации η(t), она выражается как 
. Тогда дисконтная функция выражается по формуле 
Видно, что δ(t) нелинейно выражается через {α}. Следовательно, применение сплайнов к доходности бескупонной облигации приводит к следующей экспоненциальной форме:
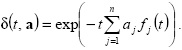
В случае
применения сплайнов для
построения мгновенной форвардной
ставки имеем 
Тогда дисконтную функцию можно выразить через форвардную ставку следующим образом:
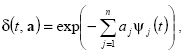
где 
Эта
функциональная форма напоминает случай, когда при помощи сплайнов строится кривая доходности бескупонной облигации,
однако выбор базисных функций отличается. Интегральная форма ведет к тому, что
базисные функции в модели являются монотонными, что предпочтительно при аппроксимации функции δ(t), которая должна монотонно
убывать с ростом t.
Для обоих этих случаев (применение сплайнов к доходности бескупонной облигации либо к мгновенной форвардной ставке) функция плотности распределения цены облигации принимает форму:
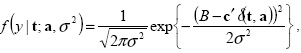
где y = B + α, 
дисконтный вектор и 
- вектор неизвестных параметров для определения на основе исходных данных.
и параметра σ2 максимизируют логарифмическую функцию правдоподобия
Ноэтому важным вопросом при использовании сплайнов является выбор количества базисных функций. Если количество базисных функций n слишком мало, тогда не удастся хорошо передать дисконтную функцию, когда она имеет сложную форму. Если же n слишком велико, дисконтная функция может чутко реагировать на «посторонние» колебания или выбросы в ущерб гладкости. В работе [4] предлагается использовать в качестве n ближайшее целое к квадратному корню из числа наблюдений.
Другой подход к решению этой проблемы -использование информационных критериев и введение штрафных членов в функцию правдоподобия [2].
Нестабильность оцененных кривых доходности всегда порождается плохой природой регрессионных сплайнов в большей степени, чем неверным выбором базисных функций [2]. Для того, чтобы избежать переопределения, в логарифмическую функцию правдоподобия вводится штрафное слагаемое. Функция правдоподобия со штрафом выглядит следующим образом:
где λ - параметр гладкости, контролирующий гладкость дисконтной функции, Δак=ак-ак-1 - оператор разности.
Задавая λ и n, неизвестные параметры a и σ2 могут быть получены путем максимизации функции правдоподобия lλ(a,σ2).Однако остается проблема - критерий, на основании которого необходимо выбирать сглаживающий параметр λ и число базисных функций n. Носкольку в функцию правдоподобия добавлено штрафное слагаемое, применение информационного критерия Акаике (Akaike Information Criteria - AIC) является теоретически необоснованным [2]. Вместо него применяется обобщенный информационный критерий (Generalized Information Criteria - GIC) [3].
СНИСОК ЛИТЕРАТУРЫ:
1. Chiu N.-C., Fang S.-C., Lavery J.E., Lin J.-Y., Wang Y. Approximating Term Structure of Interest
Rates Using Cubic L1 Splines // European Journal of Operational Research. 2008. Vol. 184. P. 990-1004.
2. Kawasaki Y., Ando T. Estimating Term Structure Using Nonlinear Splines: a Penalized Likelihood Approach // International Congress on Modeling and Simulation, section: Econometric modelling and financial econometrics. December 2005. Melbourne University, Vic P. 864-870.
3. Konishi S., Kitagawa G. Information Criteria and Statistical Modeling. Springer, 2008.
4. McCulloch J.H. Measuring the Term Structure of Interest Rates // The Journal of Business. 1971. Vol. 44. No. 1. P. 19-31.
5. Ramponi A. Adaptive and Monotone Spline Estimation of Cross-Sectional Term Structure // International Journal of Theoretical and Applied Finance. 2003. Vol. 6. No 2. P.195-212.