Введение. В современном русском языке [8, с.872] слово «управление» имеет, по крайней мере, девять различающихся смыслов. Из них применительно к факторному анализу производства подходит следующий содержательный смысл: как процесс управление - это «управлять», то есть направлять, определять поступки, поведение, взгляды и т. п. кого-либо.
При этом в общем случае возможны два крайних векторных направления поведения руководителей в процессе управления: во-первых, это управлять обстоятельствами; во-вторых, обстоятельства управляют поведением человека (в нашем случае лица, принимающего решения).
Проблема синтеза критериев. Чтобы в ходе комплексного поднятия уровня жизни у населения сельских территорий и для этого перейти от второго к первому вектору, необходимо вооружить сотрудников районной информационно-аналитической службы методологией выработки вариантных предложений и рекомендаций для лиц, принимающих решения.
В связи с этим цель данной статьи -показать несколько критериев для оценки прошлой деятельности множества сельхозпредприятий всего сельского района, необходимых при выработке вариантов управленческих решений администрацией сельского района.
Термины. Вначале приведем несколько терминов и их определений.
Критерий (от греч. kriterion - средство для суждения) - признак, на основе которого выполняется оценка. Определение или классифицирование чего-либо, мерило суждения, оценки (БСЭ, т. 13, с.450).
Критерий функционирования - обобщенный показатель, отражающий целостные свойства системы и ее функционирования. Такими критериями являются: стабильность, устойчивость, активность, интенсивность, целенаправленность, организованность, надежность, мощность, инертность, дискретность и др.
Критерий идентификации - обобщенный показатель или показатель, принятый для оценки математической модели, полученной на основе текущих статистических данных о деятельности сельхозпредприятий.
Критерий оптимальности - показатель, обобщенный показатель или критерий функционирования системы, принятые как эндогенные переменные в математической модели, т.е. как выходной результат по расчетам с помощью статистических закономерностей.
Критерий верификации (качества) -оценочная переменная, характеризующая сходимость выходных результатов модели с выходными результатами объекта исследования. Показателями в процессе верификации модели служат статистические переменные.
Критерии оптимальности и верификации в совокупности образуют критерии идентификации закономерностей через применение устойчивых законов распределения по матрице статистических данных.
Эффекты флаттера и крена. Известное в прошлом авиации явление флаттера, когда из-за сильной вибрации крылья разрушались при полете самолета, было преодолено увеличением массы по концам крыльев. Явление крена и потеря управления самолетом из-за него происходят и поныне. Оба этих явления присутствуют и в управлении производством.
На рис. 1 и рис. 2 приведены ранговые распределения по двум статистическим выборкам - материально денежных затрат МЗ по данным [9] и уровня жизни населений субъектов Российской Федерации [3].
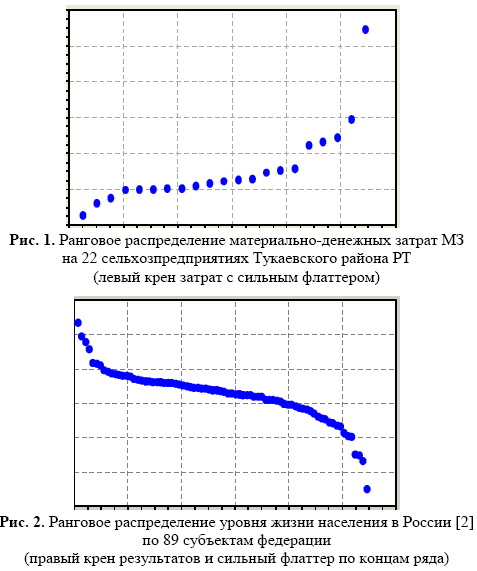
Серьезной методологической ошибкой является переход сразу же на исчисление средних арифметических величин [5]. Не только средняя температура в больнице или даже в палате, но даже и в экономических системах всякие группировки (при вычислении среднего арифметического значения вся выборка статистических данных принимается за одну группу [4]) уводят от сути изучаемого экономического явления или процесса. Эти группировки дают только новый фактор -численность наблюдений по группам статистической выборки [4, 6].
Чем меньше число групп при исчислении средних величин изучаемого фактора, то тем более огрубляется явление флаттера по концам статистического ряда. Особенно опасны деление размаха изменения значений на два, три, четыре (квартиль), пять и даже десять (дециль) групп.
Поэтому всегда вначале нужно рассматривать «поштучное распределение» значений изучаемого фактора производства. Например, по данным [6, с.36] количество начисленных за 1957 год трудодней 93 колхозникам колхоза имени Сталина Кунцевского района Московской области выглядит так, как это показано нами на рис. 3.
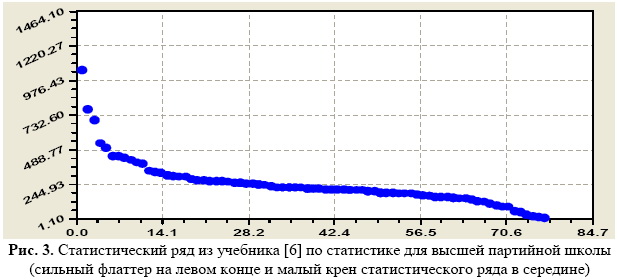
Таким образом, пара «затраты - результат» (матрица «затраты - выпуск» по В. Леонтьеву [1] или «издержки - доходы» в общей экономической теории) получает лево-правый крены, а по концам ряда происходят волновые возмущения значений фактора производства и потребления.
Критерии управления. Анализ левого и правого крена и волновых возмущений по концам ряда статистических данных позволяет рекомендовать шесть критериев для оценки эффективности процесса управления:
1. количество составляющих m статистической закономерности;
2. количество параметров n во всех составляющих модели;
3. максимальная относительная погрешность A max (по модулю) модели от фактических значений фактора в одной точке (для какого-то конкретного сельхозпредприятия);
4. значимость а каждой составляющей факторной функции;
5. коэффициент приспособляемости k системы субъектов (множества сельхозпредприятий сельского района) к внешней (экологической, политической, социальной, экономической, технологической или иной) среде;
6. коэффициент динамичности Кд системы, в данном случае субъектов производства и производственных отношений на уровне сельского района;
7. коэффициент флаттера Кф изучаемой системы, то есть коэффициент динамичности по концам ряда значений изучаемого фактора.
Эти критерии соответствуют принципу В. Леонтьева [1] об одновременности рассмотрения теории и практики: исходные данные для моделирования в виде табличной модели на данный момент времени периодически поступают от сельхозпредприятий, а районная информационно-аналитическая служба формирует закономерности рангового распределения по каждому из представленных факторов.
Результаты расчетов всех семи критериев по 22-м сельхозпредприятиям Тукаевского района Республики Татарстан приведены в табл. 1.
Далее рассмотрим каждый критерий по синтезу [7] в отдельности.
Количество m составляющих факторной функции. Этот оценочный показатель относится к структуре и функционированию производственной системы. Причем чем меньше количество составляющих, то тем эффективнее ведет себя надстройка системы субъектов производства.
Сравним два тренда, один из которых в виде линейной модели У = a1 ± a2x очень любят и применяют экономисты, а другой является наиболее распространенным в природе (то есть устойчивым) экспоненциальным законом Ципфа (в биологии), Парето (в экономике) и Мандельброта (в физике) У = a1exp(±a2x).
По первому критерию функция прямой линии уступает, так как имеет две составляющие вместо одной составляющей у нелинейного закона.
Количество n параметров статистической закономерности. Чем меньше это количество, то тем лучше «сработала» подсистема управления сельским хозяйством района, если принять за условие сравнимости (как и в случае количества составляющих) примерно равную для сравнеия сельских районов максимальную относительную погрешность Amax.
Максимальная относительная погрешность Δmax показывает не только адекватность составной модели, но и характеризует качество управления производством. При этом должно соблюдаться условие, что структурно-параметрическая идентификация исходной модели (2) проведена до максимального количества составляющих. Этот критерий является важнейшим для оценки замены табличной модели на математическую модель. Остальные четыре критерии позволяют выяснить картину поведения множества сельхозпредприятий.
Значимость α1 трендовой (среднестатистической величины, принципиально отличающейся от средних величин по [5]) закономерности факторной функции характеризует стабильность функционирования системы управления.
Этот оценочный показатель факторной функции вычисляется как отношение расчетных значений фактора производства (можно и в процентах), то есть по выражению α = y1/y или α = 100y1/y; (1), где У1 - первая (трендовая) закономерность, У - расчетное значение фактора производства по общей модели вида
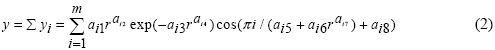
i - номер составляющей статистической закономерности, i=1,2,3...,
m - общее количество составляющих статистической модели,
r - ранг предпорядка предпочтительности у фактических значений у изучаемого фактора сельскохозяйственного производства.
Для вычислений этого и последующих критериев эффективности управления сельским районом применяется программа Excel.
Коэффициент приспособляемости к системы субъектов (множества сельхозпредприятий сельского района) к внешней среде показывает устойчивость производственной системы по отношению к различным волновым внешним и внутренним возмущениям.
Этот оценочный показатель исчисляется по формуле
![]()
где yi - первая (трендовая) закономерность, i - номер составляющей статистической закономерности, i=1,2,3...
В табл. 1 приведены значения коэффициента приспособляемости персонала сельхозпредприятий Тукаевского района к внешней экономической и иной среде функционирования сельского хозяйства. Критерий вычислен по первой волновой составляющей по формуле
![]()
Коэффициент динамичности К∂ системы, в данном случае субъектов производства и производственных отношений, показывает экономическую устойчивость сельского района в данный момент «среза» времени.
Указанный критерий вычисляется по соотношению
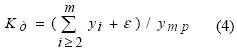
где утр - тренд, в общем случае состоящий из нескольких первых не волновых составляющих статистической модели, ε - абсолютная погрешность (остатки) модели (2).
Для нашего примера, когда трендом является только первая составляющая модели, коэффициент динамичности поведения сельского района вычисляется по формуле
где у - фактические значения изучаемого фактора производства.
Коэффициент флаттера Кф изучаемой системы, то есть коэффициент динамичности по концам (левый и правый) ряда значений изучаемого фактора может вычисляться в целом для изучаемой системы или же для левого и правого концов статистического ряда.
Для этого применяется формула
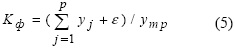
где j - номер составляющей на левом или правом концах ранжированного ряда статистической выборки, причем волновые составляющие yj будут влиять только на концы ряда статистических данных, поэтому их легко узнать в математической среде типа CurveExpert-1.3, p - количество влияющих на процесс флаттера составляющих общей статистической закономерности по ранговому распределению значений фактора производства.
В табл. 1 приведены максимальные значения (для окнкртеного из 22-х сельхозпредприятий) критерия флаттера по левому и правому краям ранжированного ряда каждого фактора сельхозпроизводства.
Удельные величины по трем факторам (МЗ, КВ и Q) к единице площади сельхозугодий (на 100 га, или все же лучше считать на один км2) дали упрощение конструкции моделей.
Поэтому далее рассмотрим эти три пары критериев.
Переход затрат в удельные материально-денежные затраты. При переходе от фактора МЗ к фактору УМЗ количество составляющих по данным табл. 1 уменьшилось с 15 до 6, то есть в 15 / 6 = 2,5 раза. Количество параметров модели снизилось в 99 / 39 = 2,54 раза.
Однако максимальная относительная погрешность возросла в 14,6 раза, хотя Amax гораздо меньше пяти процентного уровня достоверности, принятой для статистических закономерностей рангового распределения факторов сельхозпроизводства.
Значимость трендовой закономерности в обоих случаях больше 500 %, то есть велика «нагрузка» от волновых возмущений материально-денежных затрат. Но при этом коэффициент приспособляемости сельского района первой волновой функцией типа (2) при переходе к удельной величине снижается в 3,2018 / 0,6620 = 4,84 , то есть почти в пять раз. Одновременно снижается коэффициент динамичности фактора в 4,6750 / 0,8020 = 5,83 раза. Вместе с тем снижается флаттер по левой границе статистического ряда значений фактора в 3,3482 / 0,8620 = 3,88 раза, но повышается флаттер на правом конце ряда исходных данных в 0,6860 / 0,0997 = 6,88, то есть почти в семь раз. Однако преимущества редуцирования первичного фактора во вторичный (производный) налицо, поэтому оба фактора МЗ и УМЗ могут быть приняты для выявления связей между факторами сельскохозяйственного производства на уровне сельского района.
Переход квот в удельные нормы продаж сельхозпродукции. Квоты и удельные квоты значимы для кредитования сельского хозяйства. Хотя количество составляющих снизилось в 7/4=1,75 раза, а количество параметров модели (2) в 45/26=1,73 раза, однако нагрузка от волновых закономерностей на тренд возросла с 138,81 до 261,64 %. При этом требуется большая приспособляемость предприятий сельского района по удельному показателю к трендовой зависимости для всех 22-х сельхозпредприятий Тукаевского района Республики Татарстан. А коэффициент динамичности удельного фактора возросла в 0,6185 / 0,2802 = 2,21 раза.
Особую тревогу вызывает правый конец ряда предприятий с низкими удельными квотами (повышение коэффициента динамичности в 0,6184 / 0,1861 = 3,32 раза).
Этот факт указывает на недостаточную привязку объема квот КВ к площади сельхозугодий. Однако удельный фактор УКВ будет приобретать всё большую роль в управлении сельским районом и предприятиями.
Переход продукции в удельные объемы товарной продукции. Из трех рассмотренных переходов это преобразование типа Q-qS оказывается наиболее отработанным в сельском хозяйстве. Количество составляющих закономерности (2) было небольшим, но и то произошло снижение в 5 / 4 = 1,25 раза, а количество параметров факторной функции уменьшилось в 29 / 23 = 1,26 раза.
При этом точность статистической закономерности в виде суммы биотехнических функций повысилось в 2,87 / 2,22 = 1,29 раза.
Коэффициент значимости тренда снизился в 290,35 / 129,05 = 2,25 раза, а коэффициент приспособляемости администрации сельского района к управлению сельхозпредприятиями через удельный объем товарной продукции снизился в 0,5853 / 0,1608 = 3,64 раза.
Одновременно коэффициент динамичности удельного фактора уменьшился в 0,6574 / 0,2385 = 2,76 раза, снизив флаттер на правом конце ряда в 2,75 раза. Недостатком рассматриваемого перехода является увеличение флаттера на левой границе в четыре раза.
Это указывает на то, что первичный фактор товарной продукции дает уверенности крупным и богатым предприятиям, а удельный объем товарной продукции выгоден мелким и бедным сельхозпредприятиям.
Таким образом, анализ предложенных трех критериев добротности у выявленной математической модели и четырех критериев динамичности функционирования сельхозпредприятий позволяет выявить «узкие» и проблемные «места» во всей системе управления сельским районом по каждому из факторов производства.
СПИСОК ЛИТЕРАТУРЫ:
1. Леонтьев, В. Экономическое эссе. Теории исследования, факты и политика: Пер. с англ. / В.Л. Леонтьев. - М.: Политиздат, 1990. - 415 с.
2. Мазуркин, П.М. Математическое моделирование. Идентификация однофакторных статистических закономерностей: Учебное пособие / П.М. Мазуркин, А.С. Филонов. -Йошкар-Ола: МарГТУ, 2006. - 292 с.
3. Мазуркин, П. М. Распределение индекса уровня жизни (по субъектам Российской Федерации): Научное изд. / П.М. Мазуркин. - Йошкар-Ола: МарГТУ, 2006. - 56 с.
4. Мазуркин, П.М. Статистическая эконометрика: Учебное пособие / П.М. Мазуркин. - Йошкар-Ола: МарГТУ, 2006. - 376 с.
5. Маслов, П. П. Средние величины / П.П. Маслов. - М.: МФИ, 1955. - 56 с.
6. Маслов, П.П. Статистика: Учебное пособие / П.П. Маслов. - М.: Изд-во ВПШ и АОН, 1958. - 264 с.
7. Современный синтез критериев в задачах принятия решений. - М.: Радио и связь, 1992. - 120 с.
8. Современный толковый словарь русского языка / Гл. ред. С.А. Кузнецов. - М.: Ридерс Дайджест, 2004. - 960 с.
9. Шлычков, В.В. Теоретико-методологические аспекты управления ресурсным потенциалом региона / В.В. Шлычков, А. Д. Арзамасцев, Е. П. Фадеева. - Йошкар-Ола: МарГТУ, 2007. - 390 с.
Статья опубликована при поддержке гранта 3.2.3/4603 МОНРФ



