Процесс либерализации российской науки, начавшийся еще в годы Застоя и значительно ускорившийся в период Перестройки и после Августовской революции 1991 г., способствовал резкому увеличению числа исследователей, стоящих на позициях признания существования Мирового эфира (МЭ) и зачастую предлагающих новые, оригинальные модели и теории МЭ. Этот процесс продолжается и в настоящее время, несмотря на активное противодействие официальной, академической науки и отечественных и зарубежных средств массовой информации. Сейчас упоминание об идее Мирового эфира в положительном аспекте можно встретить уже не только в узко специальной научной литературе, но и в научно-популярных книгах и статьях, рассчитанных на широкий круг читателей и вышедших в нашей стране за последние два десятилетия (см., например, [8-10]). Это, несомненно, является свидетельством того, что на сегодняшний день идея МЭ вновь заняла достаточно прочные позиции.
К числу вышеупомянутых теорий Мирового эфира относится дипольно-тоннельная гидродинамическая теория гравитационного взаимодействия и электромагнитных явлений (сокращенная аббревиатура - ГТВ; подробнее см., например, [2, 5, 6, 11]), разработчиками которой являются авторы данной статьи. В процессе создания ГТВ был определен ряд параметров Мирового эфира (плотность, модуль всестороннего сжатия, а также объемные и массовые плотности электрического и магнитного зарядов, которыми обладают гипотетические «атомы» Мирового эфира, так называемые амеры). При этом в [2, 6, 11] Мировой эфир был назван «физическим вакуумом», что не меняет сути дела.
Прежде, чем перейти к описанию хода решения этой задачи, представляется целесообразным вначале остановиться на основных положениях ГТВ.
В основу ГТВ положена ламинарная (т. е., так сказать, - «безвихревая») гидродинамическая интерпретация гравитационного и электромагнитного полей (ГЭМП), что является одной из особенностей ГТВ, отличающих ее от других существующих в настоящее время теорий ГЭМП (однако следует отметить, что такая интерпретация вовсе не исключает возникновения вихреобразных турбулентностей МЭ в непосредственной близости от зарядов в результате их взаимодействий).
При гидродинамическом моделировании ГЭМП Мировой эфир представляется в виде некоторой субстанции (или вещества), имеющей сложную внутреннюю корпускулярную структуру (точнее - в виде суперпозиции ряда веществ, обладающих различными физическими свойствами). При этом и МЭ в целом, и все его компоненты рассматриваются как вещества, имеющие свойства жидкостей (т. е. сплошных сред, обладающих текучестью, а также массой и плотностью). Далее эти компоненты МЭ будем условно называть "полевыми веществами".
При этом силовые поля различной природы рассматриваются как взаимно независимые (т. е. считается, что на субъекты одного вида взаимодействия не оказывают влияния силы другой природы), что не противоречит современным представлениям и соответствующим опытным данным.
Элементарные субъекты взаимодействий (т. е. элементарные электрические заряды - в случае электрического взаимодействия; элементарные массы - в случае гравитационного взаимодействия и т.д.) при таком подходе рассматриваются как точечные источники или стоки (т. е. потребители) соответствующего полевого вещества. При этом любая реальная масса (большая элементарной массы), любой реальный электрический заряд (больший элементарного) и т. д. представляются состоящими из определенного (конечного) числа соответствующих источников или стоков. Исходя из принципа энергетической замкнутости окружающего нас пространства и закона сохранения вещества и энергии в энергетически замкнутой системе количество полевого вещества, проходящего через источники за единицу времени (т. е. суммарный расход полевого вещества через все источники), должно быть равно количеству этого вещества, проходящему через стоки за тот же отрезок времени (т.е. суммарному расходу названного вещества через все стоки).
В дальнейшем источники полевого вещества будем условно называть "а-зарядами", а стоки (потребители) -"Р-зарядами". При этом объемный и массовый расходы полевого вещества через эти субъекты взаимодействий считаются пропорциональными:
- массе материальной частицы -в случае гравитационного взаимодействия;
- величине электрического заряда -в случае электрического взаимодействия;
- величине магнитного заряда (или количеству магнетизма, используя понятия формальной теории магнетизма [7]) -в случае магнитного взаимодействия.
Результаты теоретического и экспериментального исследования взаимодействий между источниками и стоками (потребителями) как капельной, так и газообразной жидкости показывают, что а-и Р-заряды, имеющие одинаковое значение объемного расхода, в силу своих свойств (как источников и стоков полевого вещества) должны взаимодействовать между собой следующим образом:
1) два α-заряда взаимно отталкиваются;
2) два β-заряда взаимно притягиваются;
3) между α- и β-зарядами, обладающими одинаковыми значениями объемного расхода полевого вещества, не возникает никаких сил взаимодействия [1, 3, 4].
Совокупность полевого вещества и соответствующих α- и β-зарядов получила в ГТВ название "базовый полевой комплекс". Для каждого такого комплекса характерно следующее: β-заряды стремятся объединиться ("слиться") в один материальный объект; а-заряды стремятся удалиться друг от друга на максимальное расстояние.
Все виды ГЭМП могут быть представлены в виде одного или нескольких базовых полевых комплексов. В последнем случае:
1) все базовые полевые комплексы, используемые для моделирования данного типа силового взаимодействия, должны рассматриваться как взаимно независимые (т. е. заряды одного комплекса не взаимодействуют с зарядами другого комплекса, и наоборот);
2) материальные объекты, являющиеся субъектами данного взаимодействия (электрического, магнитного и т. д.), представляются в виде комплекса α- и (или) β-зарядов, относящихся к различным базовым полевым комплексам.
Сравнительный анализ формул, полученных в классической физике (с одной стороны) и в ГТВ (с другой стороны) для сил, возникающих при гравитационном, электрическом и магнитном взаимодействиях, показывает, что полная идентичность этих формул достигается в том случае, если рассматривать МЭ в целом и все его компоненты, участвующие в гравитационном, электростатическом или магнитостатическом взаимодействии, как вещества, обладающие свойствами несжимаемых жидкостей, т.е. когда рF=соnst;при R=var, где ρF - плотность МЭ; ρF=1,192*109 кг/м3(см. [2, 5, 11]); R - расстояние от гравитационного, электрического или магнитного заряда до рассматриваемой точки пространства. Если при этом пренебречь потерями энергии в потоке МЭ, то можно воспользоваться уравнением Бернулли для объемной плотности энергии идеальной жидкости. В соответствии с этим уравнением полная удельная энергия (т. е. объемная плотность полной энергии) eF потока МЭ на расстоянии R от того или иного заряда (в любом направлении от последнего) при z=0 определяется следующим образом:
где
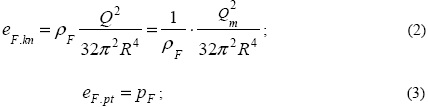
eFkn и eFpt - составляющие полной удельной энергии МЭ, т.е. объемные плотности (удельные значения) соответственно кинетической и потенциальной энергий, которой обладает МЭ на расстоянии R от соответствующего заряда; z - геометрический напор; Q, Qm - соответственно объемный и массовый расход МЭ через данный заряд; Qm = PF · Q; PF - давление в МЭ на расстоянии R от заряда;
![]()
Величины Q и Qm связаны с соответствующим гравитационным, электрическим или магнитным зарядом q следующим образом:

где ![]() ; для гравитационного взаимодействия
; для гравитационного взаимодействия ![]() ; для электростатического взаимодействия
; для электростатического взаимодействия ![]() ; для магнитостатического взаимодействия
; для магнитостатического взаимодействия![]() ; G,
ε0, μ0 - гравитационная, электрическая
и магнитная постоянные соответственно.
; G,
ε0, μ0 - гравитационная, электрическая
и магнитная постоянные соответственно.
Сравнительный анализ уравнения (1) и аналогичных математических выражений из классической физики позволяет сделать следующие выводы:
1. Объемная плотность энергии МЭ имеет одно и то же значение на любом удалении от заряда и ни при каком значении R не стремится к бесконечности. Тем самым при таком представлении (т.е. при гидродинамической интерпретации) гравитационного и электромагнитного взаимодействий в ГТВ проблемы бесконечностей не возникает.
2. Полная энергия МЭ (а также и полная энергия поля, заряда) складывается издвух составляющих потенциальной.
3. В классической физике при определении энергии электрического заряда и других объектов учитывается не вся полная энергия последнего, а лишь одна (кинетическая) ее составляющая, которая неограниченно возрастает при уменьшении расстояния до рассматриваемого объекта (при этом в рассмотрение не принимается потенциальная составляющая указанной полной энергии, т. е. давление в МЭ). Именно этим и объясняется возникновение проблемы бесконечных энергий в классической физике (см. рис. 1, где e - объемная плотность энергии; значение Rc определяется из (1) с учетом (2) при eF.pt=0).
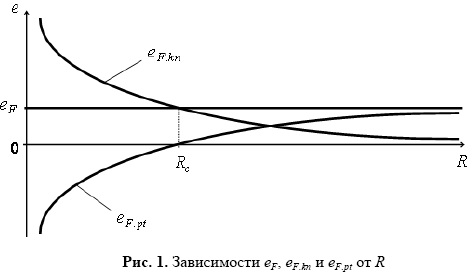
Теперь перейдем к
определению величины eF и ее составляющих eF.kn и eF.pt. Значение eF.kn определяется в соответствии с (2), (5) и (6) с учетом
значения ρF, приведенного выше.
Значение eF может быть определено из (1) с использованием общеизвестной формулы, связывающей между собой массу, энергию и скорость света и имеющей вид
![]()
где (в рассматриваемом частном случае) Wf- полная энергия МЭ; m - масса МЭ; c - скорость света в МЭ.
В ГТВ свет рассматривается как волна деформации Мирового эфира, носящая смешанный продольно-поперечный характер (в отличие от обычных продольных и поперечных волн). Любая деформация МЭ (по представлениям ГТВ) должна сопровождаться одновременным изменением не только электромагнитного, но и гравитационного полей (в силу особенностей физических свойств так называемых амеров - частиц, из которых состоит МЭ, геометрические размеры которых на много порядков меньше размеров мельчайших элементарных частиц). Таким образом, в соответствии с ГТВ свет - это не только электромагнитная, но и гравитационная волна.
Выше было отмечено, что проведенные исследования однозначно указывают на то, что МЭ по своим свойствам близок к идеальной (т.е. несжимаемой и невязкой) жидкости [1, 2, 11 и др.]. В связи с этим скорость света может быть определена по известной формуле для скорости распространения волны деформации, которая в нашем случае будет иметь следующий вид (см., например, [12]):
Подставив (8) и выражение для ρf в (7), получаем следующее:
Отсюда:
Из уравнения (1) следует, что величина efpt может быть определена по формуле
В соответствии с (3) и (11) давление pfo в невозмущенном МЭ (т.е. давление в точке, удаленной на бесконечно большое расстояние от всех зарядов - гравитационных, электрических, магнитных) равно ef pt при R →∞, т.е.
![]()
Прежде, чем перейти к другим физическим параметрам МЭ, отметим, что гидродинамическая интерпретация ГЭМП позволяет понять физический смысл гравитационной, электрической и магнитной постоянных (в отличие от других физических теорий, которые лишь констатируют факт существования Мировых констант, никак их не объясняя). В процессе работы по созданию ГТВ авторами данной статьи было получено универсальное (обобщенное) выражение для силы, возникающей при гравитационном, электростатическом или магнитостатическом взаимодействии, все переменные в котором имеют ясный физический смысл (см., например, [11]):
или
где
или
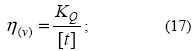
где F - сила, действующая на два
субъекта рассматриваемого взаимодействия (при этом индексами «1» отмечены величины,
имеющие отношение к первому субъекту, а индексами «2» - величины, относящиеся
ко второму субъекту взаимодействия); r - расстояние между объектами
взаимодействия (т.е. между зарядами q1 и q2); i принимает значение 1 для первого субъекта
рассматриваемого взаимодействия и значение 2 для второго субъекта данного
взаимодействия; h(v) - объемная плотность заряда qi того или иного вида (электрического, магнитного или
гравитационного); η(m) -
массовая плотность заряда
qi; ![]() ,
, ![]() , V - объем; M -
масса; [t] -
, V - объем; M -
масса; [t] -
величина, численно равная единице, а ее размерность совпадает с размерностью времени (т.е. в системе СИ - [t] = 1 с);
KQm - коэффициент пропорциональности между массовым расходом МЭ (или соответствующего компонента МЭ, если речь идет о кулоновском взаимодействии) через данный заряд и величиной этого заряда; KQ - коэффициент пропорциональности между объемным расходом МЭ (или соответствующего компонента МЭ, если речь идет о кулоновском взаимодействии) через данный заряд и величиной этого заряда.
В качестве заряда qi может выступать (в данном, конкретном рассматриваемом случае; в зависимости от вида фундаментального взаимодействия) либо электрический заряд, либо магнитный заряд, либо масса некоторого материального объекта (гравитационный заряд), т.е.: qi = Mi,или qi ≡ qEi, или qi ≡ qMi, где qE - кулоновский заряд; qM - магнитный заряд (количество магнетизма).
Здесь следует сделать два замечания-пояснения. Во-первых, понятие "магнитный заряд" (или, иначе, - количество магнетизма) на протяжении уже многих десятилетий широко используется в общепринятой формальной теории магнетизма; см., например, [7]. Во-вторых, ГТВ позволяет понять физический смысл понятия «масса»: под массой (например, некоторого тела) в ГТВ понимается масса вещества МЭ, поглощаемого (если речь идет о веществе - противоположности антиматерии) или испускаемого (если речь идет об антивеществе) данным объектом за единицу времени (т.е. за интервал времени, равный величине [t] ).
Как было отмечено выше, в ГТВ Мировой эфир рассматривается как вещество, представляющее собой смесь корпускул, равномерно распределенными в пространстве и отличающимися друг от друга некоторыми физическими свойствами. Общим для них является то, что все они обладают массой. Кроме того, часть из них обладает электрическим зарядом (того или иного вида), а часть из них - магнитным зарядом (или, иначе, - количеством магнетизма того или иного вида). То есть, в соответствии с такой моделью МЭ представляет собой "равномерную смесь" всех видов электрических и магнитных зарядов, что объясняет его электрическую и магнитную нейтральность (в частности, в невозбужденном состоянии).
Для такой модели МЭ в результате анализа полученных в работе формул с использованием Мировых констант, а также совместного решения соответствующих уравнений был определен ряд физических параметров МЭ, приведенных в табл. 1 вместе с теми параметрами, речь о которых шла выше в данной статье.
В этой таблице использованы следующие обозначения: ηE(v), ηM(v)-объемные плотности электрического и магнитного зарядов МЭ соответственно (т.е. отношение величины заряда к занимаемому им oбъему); ηе(m), ηM(m)-массовые плотности электрического и магнитного зарядов МЭ соответственно (т.е. отношение величины заряда к массе заряда; очевидно, что в случае гравитационного заряда ηM(m) = 1); βf - коэффициент объемного сжатия (коэффициент сжимаемости) МЭ. Величина G* численно равна гравитационной постоянной (постоянной Кавендиша G), а ее размерность - м3 /кг, т.е.
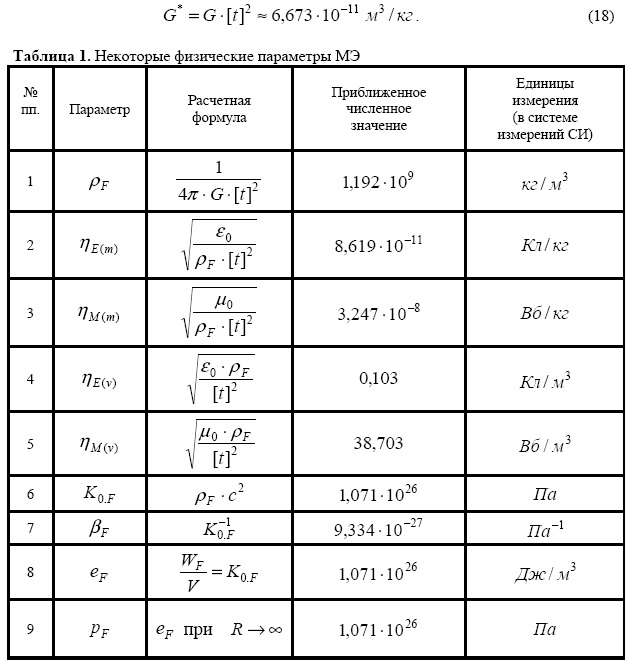
Из (18) и формул, приведенных в табл. 1, могут быть получены следующие выражения для Мировых констант, все переменные в которых имеют ясный физический смысл:
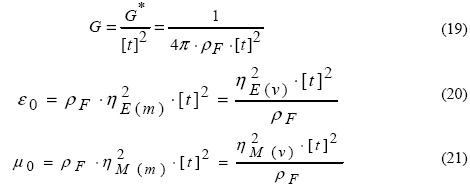
Из формул (19)-(21) следует, что все три Мировые константы (G,ε0 и μ0) характеризуют определенные физические свойства МЭ, а именно:
- гравитационная постоянная G характеризует плотность Мирового эфира (точнее, - объемную плотность вещества МЭ);
- электрическая постоянная ε0 характеризует комплексную объемно-массовую плотность распределения электрических зарядов в веществе МЭ;
- магнитная постоянная до характеризует комплексную объемно-массовую плотность распределения магнитных зарядов (или, иначе, - количества магнетизма) в веществе МЭ.
Таким образом, в ходе выполнения данной работы получены значения ряда физических параметров МЭ. С учетом этих величин выражения (1)-(3), (13) и (14) могут быть использованы для моделирования (расчета) полей давлений и скоростей движения амеров в массиве МЭ для любого комплекса материальных объектов.
СПИСОК ЛИТЕРАТУРЫ:
1. Бражников А.В. Гидродинамическое моделирование силовых взаимодействий. -Красноярск: Издательство КГАЦМиЗ, 1997. -32 с.
2. Бражников А.В., Минеев А.В. Основы гидродинамической теории фундаментальных взаимодействий // Сборник научных трудов
«Вестник университетского комплекса». -Красноярск: Издательство ВСФ РГУИТП, НИИ СУВПТ. - Вып. 3 (17), 2005. - С. 191-19.
3. Бражников А.В., Хомич Л.В., Хоменко А. В. К вопросу о силах, возникающих при движении жидкости // Сборник материалов межвузовской научно-практической конференции «Инновационные процессы в современном образовании России как важнейшая предпосылка социально-экономического развития общества». - Красноярск: Издательство ГУЦМиЗ, 2006. - С. 178-180.
4. Бражников А.В., Гилев А.В., Довженко Н.Н., Хомич Л.В. Поведение гидроаэромеханических сил при малых расстояниях между потребителями жидкости // Сборник материалов межвузовской научно-практической конференции «Инновационные процессы в современном образовании России как важнейшая предпосылка социально-экономического развития общества». - Красноярск: Издательство ИЦМиЗСФУ, 2007. - С. 267-271.
5. Бражников А.В., Гилев А.В., Белозеров И.Р. Факты, свидетельствующие в пользу дипольно-тоннельной гидродинамической теории гравитационного взаимодействия и электромагнитных явлений // Фундаментальные исследования. - № 5 (приложение),2009. - С. 9-10.
6. Животов Д.В., Бражников А.В., Хомич Л. В. Решение проблемы бесконечностей в гидродинамической теории гравитационного взаимодействия и электромагнитных явлений // Сборник материалов Всероссийской научно-технической конференции «Совершенствование технологий производства цветных металлов». - Красноярск: Издательство ГУЦМиЗ, 2005. - С. 17-19.
7. Калашников С.Г. Электричество. - М.: Наука, 1964. - 668 с.
8. Новицкий В. «Камень преткновения» в физике? // Техника - молодежи. - № 5, 1990. - С. 18-21.
9. Пономарев В.Т. История оружия: вчера, сегодня, завтра. - Ростов-на-Дону: Феникс, 2007. - 272 с.
10. Разомасов П. Разгадка гравитации - в элементарной частице // Сегодняшняя газета. - Красноярск, № 15 (1100), 31 января 2000 г. - С. 13.
11. Юмшин Д.В., Бражников А.В., Хомич Л.В. Основные положения гидродинамической теории гравитационного взаимодействия и электромагнитных явлений // Сборник материалов межрегиональной научной конференции «Молодежь и наука - третье тысячелетие». - Красноярск: Издательство КРО НС«Интеграция», 2005. - С. 260-265.
12. Яворский Б.М., Детлаф А.А. Справочник по физике. - М.: Наука, 1980. - 512 с.



