Завершающим этапом факторного анализа является выявление бинарных отношений между факторами, в нашем случае факторами сельскохозяйственного производства.
Дальнейшее развитие теории идентификации устойчивых законов позволит выявлять статистическим моделированием биотехнические закономерности и по более сложным взаимоотношениям между отдельными факторами.
В классической теории производства используются слишком упрощенные модельнотеоретические представления, как правило, линейные закономерности, действительные только на короткие промежутки времени, но никак не объясняющие долговременные явления и явно нелинейные процессы. Причем анализ динамики эконометрических публикаций, например [1], за вторую половину ХХ века показывает, что постепенно ученые отказались от полиномов (чаще всего применялось квадратное уравнение, не имеющее содержательного смысла). Но зато возросли математические ухищрения по аппроксимации этими линейными моделями явно нелинейных по своей сути закономерностей (например, линеаризация, кусочнолинейные аппроксимации, линейные тренды с остатками и пр.).
До сих пор модельнотеоретические представления теории производства не получили четких описаний в виде математически выраженных законов и закономерностей. Топтание на месте классической эконометрики и даже откат обратно к линейным закономерностям без учета нелинейности моделей объясняется тем, что современная математическая статистика оперирует законом больших чисел и законом нормального распределения (законом Гаусса-Лапласа) независимых величин.
Математическая статистика оказалась действенной в технических науках, но даже там не может справиться с взаимозависимыми факторами. Математики любят приводить классический пример с измерениями диаметра вала, но просто забывают, что с учетом изменения свойств измеряющего человека (усталость во времени, начало, середина или конец смены и пр.) распределение диаметра вытачиваемых валов становится ненормальным, то есть не подчиняющимся закону ГауссаЛапласа. Поэтому классическая статистика во многом бессильна изза слепого подражания методам классической высшей математики.
Если в конце XIX века был безоговорочный диктат математики над статистикой, то в начале ХХ! века пришло неосознанное понимание безысходности такой доктрины. В ближайшие годы будет осознанный переворот: статистика станет первой, а математика второй по научнопрактической значимости [25].
Чтобы лучше был понятен процесс выявления связей между зависимыми друг от друга факторами производства (что является принципиально новым) приведем некоторые термины и их определения.
Объясняющая переменная переменная, которая объясняет причинные связи в явлении или процессе (относится к экзогенным факторам).
Значение переменной количественное или качественное выражение отличительной характеристики.
Показатель оценочная переменная, которая характеризует следствие, то есть оценивает выходной результат функционирования эргатической (то есть объекта исследования с включением человека) системы.
Отсюда следует, что общее число переменных в моделях равно сумме параметров модели, объясняющих переменных и показателей. Исследователь превращает некоторые переменные в параметры только вследствие недостаточности априорных и апостериорных знаний. Поэтому параметры модели, соответственно коэффициенты и эмпирические коэффициенты, имеют реальный прямой и косвенный смысл. Каждое число в математической модели это не просто «число» как счетная единица, а число со смыслом как «вещь в себе».
Целевой показатель оценочная переменная, полученная на основе программноцелевых исследований целей и прогнозных сценариев будущих состояний экономической или иной системы.
Плановый показатель оценочная переменная, по которой для эргатической системы, то есть для системы с включением людей (например, сельскохозяйственное предприятие), устанавливают плановые задания.
Директивный показатель оценочная переменная, значение которой контролируется вышестоящими по иерархии эргатическими системами. Оптимальной является ситуация, когда целевые, плановые и директивные показатели совпадают по номенклатуре и значениям на одинаковый период упреждения производственной деятельности. В реальных условиях эти множества взаимно пересекаются и расходятся друг от друга все больше при повышении неадекватности системы управления.
Собственный показатель оценочная переменная, используемая для описания поведения только данной конкретной эргатической системы.
Для множества однородных эргатических систем общее множество составляется объединением (дизъюнкцией) конкретных множеств собственных показателей. Они характеризуют, как правило, внутреннее функционирование системы и, как правило, не относятся к директивным и плановым показателям (частично относятся к целевым показателям).
Для бинарных отношений [6] берутся первичные и производные от них действенные факторы. Производные от нескольких первичных факторов переменные исключаются.
Например, в работе [7, с.147] был предложен фактор производственный потенциал. Однако он вычислен как средневзвешенное значение от четырех факторов производства: балла оценки сельскохозяйственных угодий (СХУ); удельной стоимости основных производственных фондов (УОПФ) на единицу площади СХУ; удельных материальноденежных затрат (УМЗ) на единицу площади СХУ; удельного персонала, то есть среднегодовой численности работников на единицу площади СХУ. Все эти четыре фактора присутствуют в табл. 1, поэтому искусственный фактор под названием «производственный (ресурсный) потенциал» исключается из множества учитываемых переменных.
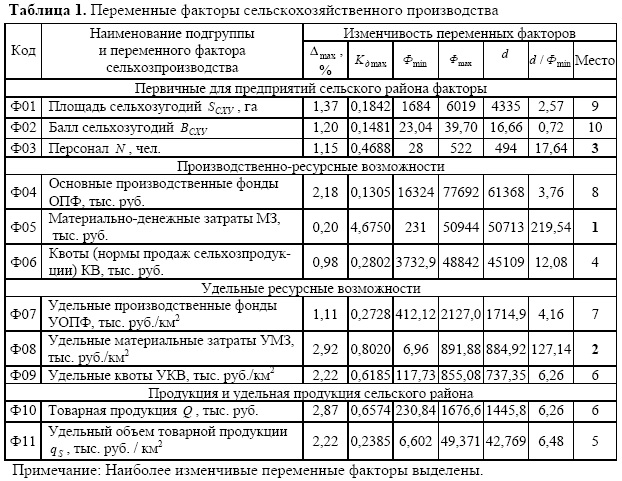
В табл. 1 приведены следующие условные обозначения: Δmax максимальная относит ельная погрешность статистической модели от фактических значений фактора в одной точке; K∂max максимальный коэффициент динамичности во множестве субъектов производства и производственных отношений; Фmin минимальное количественное значение переменного фактора; Фmах максимальное количественное значение фактора; d - размах значений фактора, причем d = Фmax-Фmin.
Из списка переменных исключены также те производные факторы, например, «удельный персонал», которые имели более сложные по сравнению с первичными факторами модели рангового распределения. Исключены из списка переменных ранговые факторы производства. Модели ранговых распределений вполне позволяют отобрать группу переменных факторов, участвующих в поиске моделей взаимосвязи.
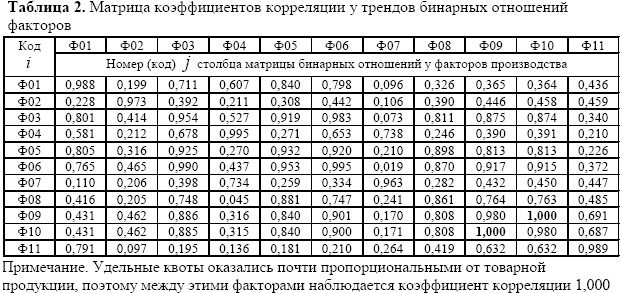
По схеме [6] в табл. 2 приведена квадратная матрица для анализа бинарных отношений между всеми 11 переменными величинами.
Взаимосвязь фактора от самого себя определяется ранговым распределением, то есть монарным отношением.
По всем монарным и бинарным сочетаниям факторов сельскохозяйственного производства были получены статистические закономерности
Взаимосвязь фактора от самого себя определяется ранговым распределением, то есть монарным отношением.
По всем монарным и бинарным сочетаниям факторов сельскохозяйственного произво дства были получены статистические закономерности.
Хотя в экономической литературе немало сведений о влиянии тех или иных факторов на другие, однако предположим, чт о пусть мы не знаем содержание всех клеток бинарных отношений типа Фi = f(Фj), где i (по строкам) и j (по столбцам)-номера переменных факторов, участвующ их в бинарных отношениях.
В каждую клетку табл. 2 можно поместить формулу и графики, полученные по данным табл. 3 в программной среде CurveExpert1.3.
Теперь можно определиться с уровнями коэффициента корреляции. На рис. 1 приведены шесть случаев по уровням адекватности полученных биотехнических закономерностей: а) коэффициент корреляции трендов не меньше 0,500; б) не менее 0,600; в) от 0,700 и выше; г) от 0,800 и более; д) от 0,900 и более; е) равный 1,000.
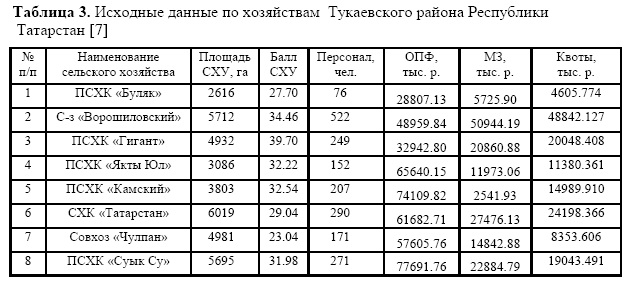
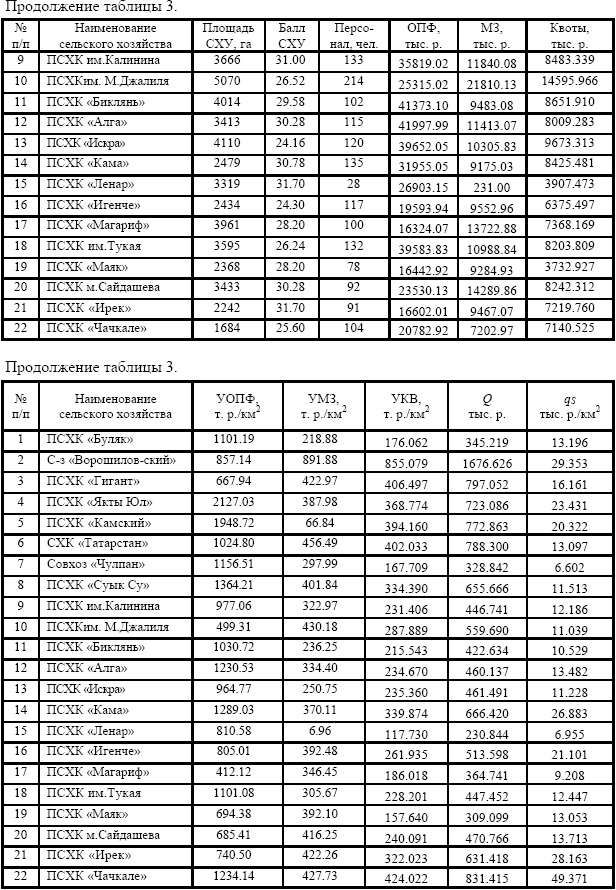
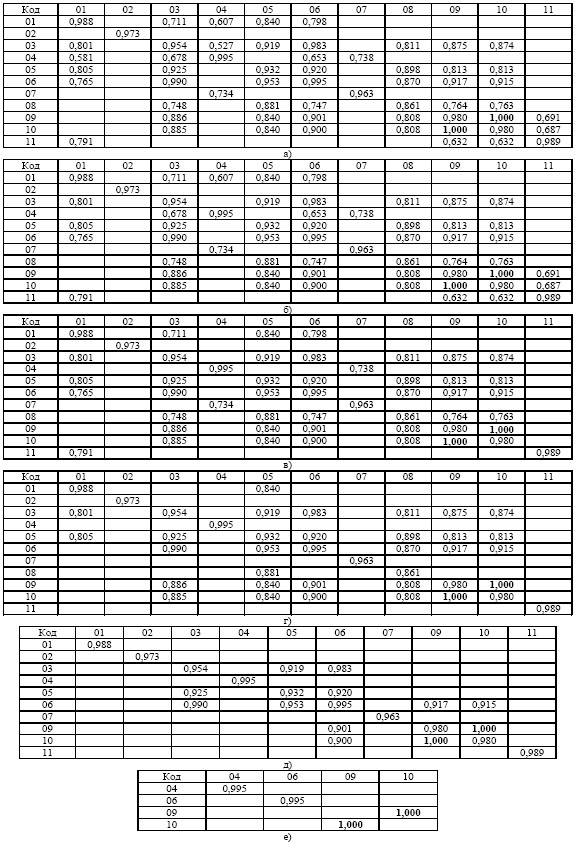
Рис. 1. Распределение коэффициента корреляции трендов по уровням значимости: а) коэффициент корреляции трендов не меньше 0,500; б) не менее 0,600; в) от 0,700 и выше; г) от 0,800 и более; д) от 0,900 и более; е) 1,000
Таким образом, для одного сельского района будет составлена математическая модель, включающая в себя 121 формулу. В работе [6] указывается, что для описания экономики страны требуется до 3000 эмпирических моделей, встроенных в общую экономикоматематическую модель. Для России мощность комплекса статистических моделей будет равна 121 * (количество сельских районов + 88 субъектов федерации + 7 федеральных округов + 1 страна в целом). Всё это множество «портретов поведения» сельского хозяйства можно разделить по природноэкономическим, дорожноклиматическим и иным зонам.
При этом каждый сельский район получит свою специфическую матрицу типа табл. 2. Однако многие сельские районы из различных субъектов Российской Федерации будут иметь примерно одинаковые «портреты поведения». Группируя их, можно составить типизацию производственных отношений (то есть типов стиля производственного поведения) среди сельхозпредприятий в сельских районах. Таковы вкратце перспективы применения матриц типа табл. 2, со своими трендами по всем клеткам, которые могут быть помещены в различные вычислительные программы (имитационные модели), например, для точного прогнозирования на следующий год возможностей и результатов сельской деятельности.
Из схем на рис. 1 е видно, что максимальную адекватность имеют взаимосвязи УКВ = f(Q) и Q = /(УКВ) по следующим формулам статистических закономерностей (рис. 2):
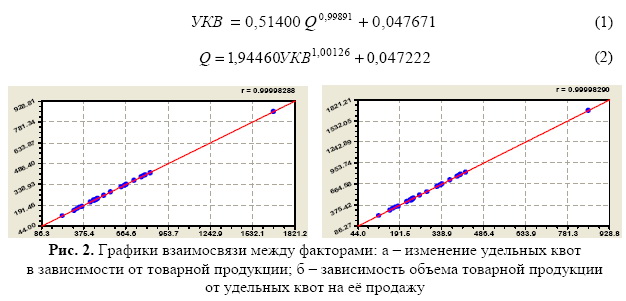
По схеме на рис. 1 е одинаковый коэффициент корреляции 0,995 получили два фактора по ранговым распределениям своих значений (рис. 3): а) основные производственные фонды (Ф04)
б) квоты, то есть нормы продаж сельхозпродукции (Ф06)
где rопф, rкв ранги значений факторов производства, расставленные по предпорядку предпочтительности (по возрастания ОПФ и убыванию КВ, по вектору ухудшения).
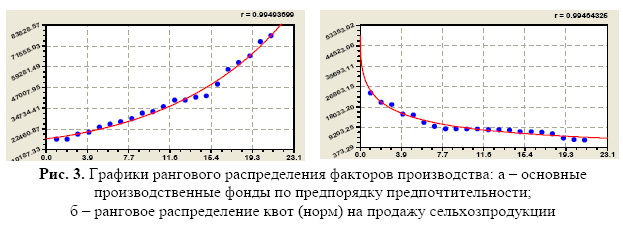
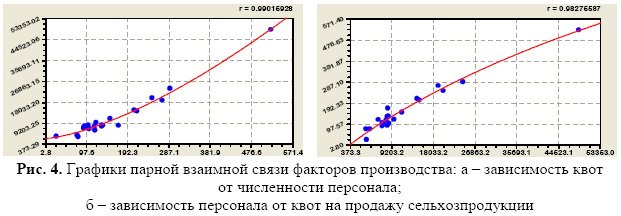
Статистические закономерности бинарных отношений факторов, полученные на основе применения устойчивых законов, как правило, всегда отличаются от простейших линейных зависимостей. После идентификации биотехнического закона [25] получены:
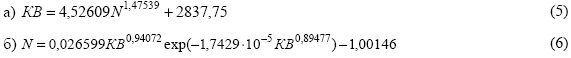
Формула (5) позволит районной информационноаналитической службе рекомендовать выделение квот на продажу продукции по численности персонала сельхозпредприятий.
Одновременно на предприятиях повысится качество управления персоналом. Взаимное влияние материальноденежных затрат и квот определяется уравнениями:

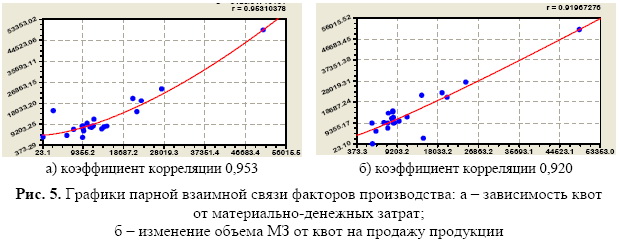
Если квоты известны по
(5), то, подставляя результаты вычислений в формулу (8), можно получить объем
возможных материальноденежных затрат по сельхозпредприятиям.
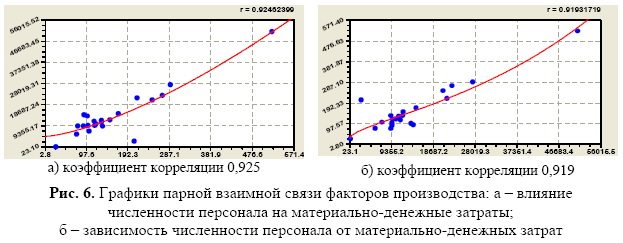
Можно определить материальноденежные затраты через численность персонала, так как в принятие квот могут вмешаться личные связи. Для этого получены формулы (действительны только для конкретного сельского района результатам прошлого учетного периода):
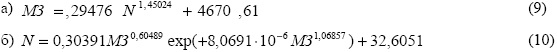
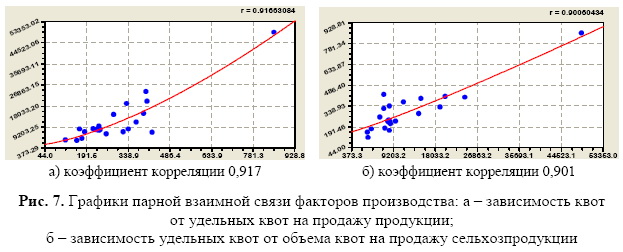
Интерес представляют взаимные связи между квотами и их удельными величинами на единицу площади СХУ. Получены формулы статистических закономерностей:

В этих формулах (11) и (12) могут быть скрыты профессиональные тайны тех, кто принимает решения о тех или иных квотах на основе удельных квот, зависящих от объема товарной сельхозпродукции.
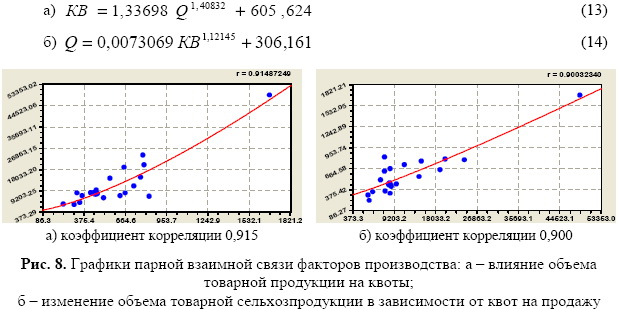
Для бинарных связей между родственными факторами производства (квоты это предполагаемая еще до проведения сельскохозяйственных работ на будущее цикла воспроизводства товарной продукции) получены уравнения (рис. 8):
Таким образом, трендовые закономерности однотипны и содержат две составляющие:
- постоянный член, показывающий уровень не влияния того или иного фактора, то есть при возможном теоретически нулевом значении объясняющей переменной;
- переменный по биотехническому закону (или его частным случаям) член закономерности, показывающий непосредственное влияние объясняющей переменной на фактор, принятый как показатель.
С учетом формул (1) и (2) показателями сельхозпроизводства на уровне сельского района могут стать факторы УКВ, Q, КВ, N и МЗ по убыванию коэффициента тесноты взаимной связи (корреляции, а лучше считать корреляционное отношение). В дальнейшем необходимо многофакторное моделирование указанных показателей сельхозпроизводства.
Предлагаемая методология факторного анализа позволит повысить качество экономического управления сельским хозяйством на различных уровнях администрирования. В особенности предложенная методология будет значимой на уровне управления сельхозпредприятиями сельского района.
СПИСОК ЛИТЕРАТУРЫ:
1. Математическое моделирование экономических процессов в сельском хозяйстве / А.М. Гатаулин, Г.В. Гаврилов, Т.М. Сорокина и др.; под ред. А.М. Гатаулина. М.: Агропромиздат, 1990. 432 с.
2. Мазуркин, П.М. Геоэкология: Закономерности современного естествознания: Научное изд. / П.М. Мазуркин. ЙошкарОла: МарГТУ, 2006. 336 с.
3. Мазуркин, П. М. Закономерности загрязнения природы / П.М. Мазуркин,Е.А. Щербакова: Научное издание. Йошкар-Ола: МарГТУ, 2002. 62с.
4. Мазуркин, П.М. Математическое моделирование. Идентификация однофакторных статистических закономерностей: Учебное
пособие / П.М. Мазуркин, А.С. Филонов. ЙошкарОла:
МарГТУ, 2006. 292 с.
5. Мазуркин, П. М. Статистическая эконометрика: Учебное пособие / П.М. Мазуркин. ЙошкарОла: МарГТУ, 2006. 376 с.
6. Саати, Т. Принятие решений: Метод анализа иерархий: Пер. с англ. / Т. Саати. М.: Радио и связь, 1993. 320 с.
7. Шлычков, В.В. Теоретикометодологические аспекты управления ресурсным потенциалом региона / В.В. Шлычков, А.Д. Арзамасцев, Е.П. Фадеева. Йошкар-Ола: МарГТУ, 2007. 390 с.
Статья опубликована при поддержке гранта 3.2.3/4603 МОНРФ



