Введение. Факторы производства, рассматриваемые в данной статье в области сельского хозяйства на уровне множества сельхозпредприятий сельского административного района, имеют особенности, связанные больше всего с деятельностью людей, то есть с так называемым «человеческим фактором», чем с природными явлениями и процессами.
Проблема факторного анализа. Динамичность факторных функций значительна и показывает поведение субъектов сельского хозяйства больше «по понятиям», чем по научным обоснованиям. Изза этого велика роль в производственных отношениях личности руководителя сельхозпредприятия. В связи с этим проблема выявления и применения закономерностей изменения количественных значений у факторов производства имеет актуальную новизну. Система закономерностей факторных функций производства приобретает важную научную и практическую роль в свете намечаемых мер по комплексному возрождению производственных отношений на сельских территориях.
Исходные предпосылки. Вначале приведем основные термины и их определения:
закон объективная связь, устойчивое отношение между явлениями и процессами;
закономерность зависимость, подчиненная закону, объективная связь.
Известные в экономике законы и закономерности дополняют и усиливают функциональные (теоретические) модели, поэтому дедуктивное и индуктивное объединяются в общем процессе, в котором статистическое моделирование приобретает весомую значимость.
Статистическая закономерность одна из форм проявления закономерной связи между предшествующим и последующим состояниями системы. Данное состояние системы определяет ее будущее состояние не однозначно, а лишь с определенной вероятностью, являющейся объективной мерой возможности реализации заложенных в прошлом тенденций изменения системы [1, с.496].
В нашем случае факторы производства рассматриваются относительно самого себя (факторный анализ сельскохозяйственного производства) по закономерностям рангового распределения. Поэтому в дополнение к вышеприведенному определению вполне существуют формы проявления закономерной связи и для какогото момента времени, то есть в конкретном «срезе» времени. Причем «срезы» времени могут быть по прошлым (для прогнозирования), настоящим (оперативное управление) и будущим (факторный анализ проектов будущего) статистическим данным.
Математическая модель (БСЭ, т. 15, с.480481) приближенное описание какоголибо класса явлений внешнего мира, выраженное с помощью математической символики.
Анализ математической модели позволяет проникнуть в сущность изучаемых явлений. Процесс математического моделирования, как правило, включает в себя этапы:
1. формулировка законов, связывающих объекты модели, знание фактов;
2. исследование математических задач, к которым приводят математические модели: решение прямой задачи, то есть выходных результатов математической модели для дальнейшего сопоставления с результатами наблюдений за изучаемым явлением или процессом, применение вычислительной техники;
3. выяснение того, удовлетворяет ли принятая модель критерию практики, то есть адекватности модели: если отклонения выходят за пределы принятой точности соответствия математической модели практике, то такая модель не может быть принята;
4. анализ математической модели в связи с накоплением дополнительных научных данных и модернизация этой модели.
Формула (лат.: форма, правило) представление связей, отношений, существующих между предметами (явлениями, процессами) при помощи знаков (символов), объединенных определенными математическими и логическими действиями.
Общая модель. В общем случае каждый член статистической модели может быть описан так называемой биотехнической вейвлетфункцией проф. П.М. Мазуркина [24] типа
![]()
где y - изучаемый фактор, принятый как количественная характеристика исследуемого явления или процесса, x - объясняющий фактор с количественными значениями, a1... a12 - параметры модели, принимающие числовые значения в ходе идентификации формулы (1) в зависимости от отличительных особенностей конкретного изучаемого явления или процесса.
Для факторов производства характерны условия a6=0, a7=1, a10=0 и a11=1. Поэтому для факторного анализа в сельском хозяйстве получаем уравнение вида
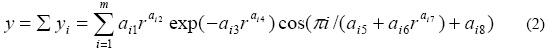
где y - изучаемый фактор производства, i - номер составляющей статистической закономерности, i=1,2,3... , m - общее количество составляющих статистической модели, r - ранг предпорядка предпочтительности у фактических значений y€ изучаемого фактора сельскохозяйственного производства. Причем принимается предпорядок r=1,2,3... по вектору направленности значений фактора в сторону ухудшения, то есть ранжирование значений изучаемого фактора выполняется по принципу «от лучшего к худшему».
Все 20 выявленных факторов производства сельхозпредприятий Тукаевского района Республики Татарстан [5] нами были разделены на пять подгрупп и их математические модели (статистические модели + ограничения по правой границе рангов) приведены в нижеследующих таблицах.
Первичные для предприятий сельского района факторы. В табл. 1 приведены значения параметров модели (2). При этом знаки перед составляющими образуются по знакам соответствующих параметров.
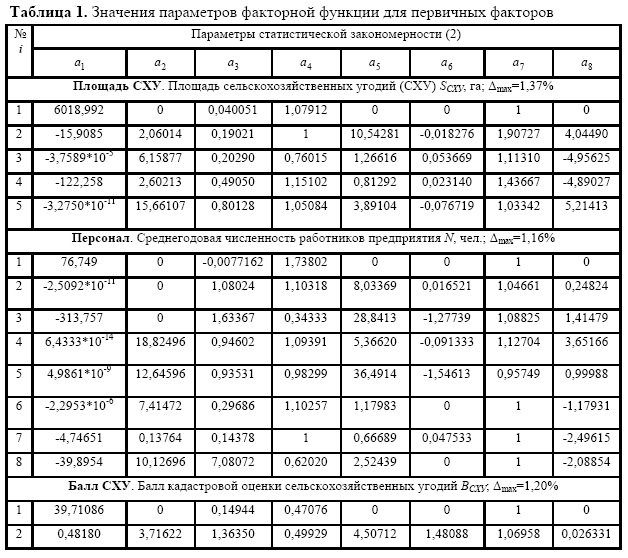
Фактор персонала после идентификации модели (2) получила восемь составляющих. Во всех 20 закономерностях только первая составляющая не является волновой функцией.
Таким образом, все составляющие большинства статистических моделей факторов производства, как показано в табл. 1 и других, могут иметь матрицу из 8 параметров (по строкам) и по количеству m составляющих (по столбцам) статистической модели (2). Производственноресурсные возможности. К этой подгруппе относятся пять факторов производства (табл. 2).
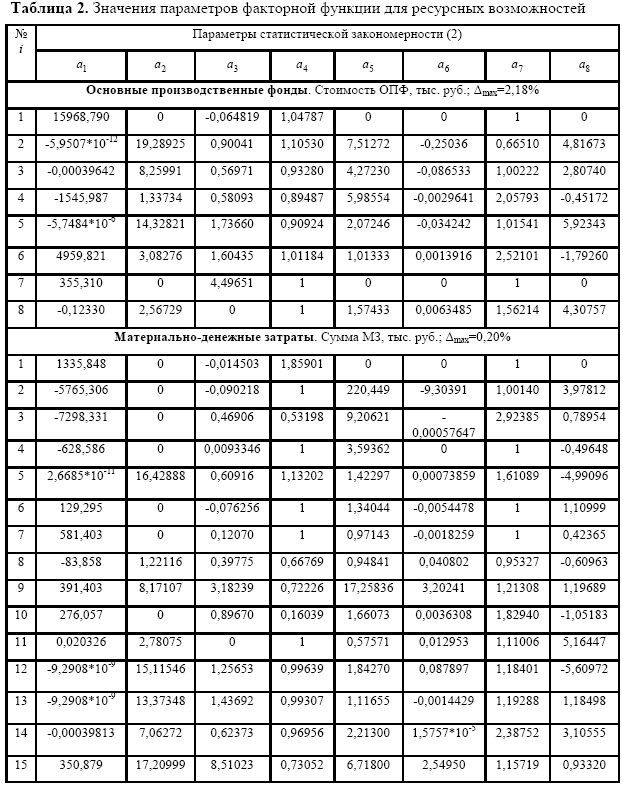
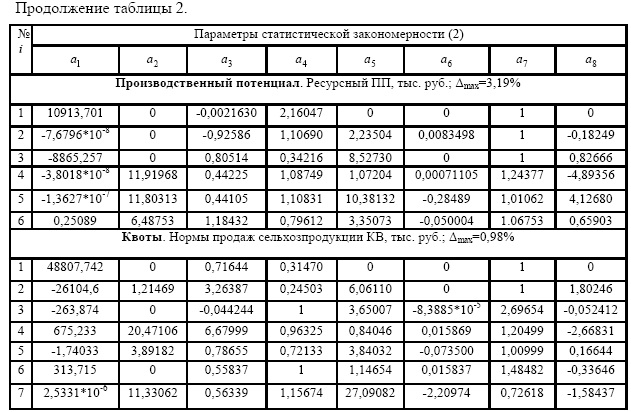
Наибольшее количество составляющих m=15 имеет фактор «материальноденежные затраты». Остальные факторные функции имеют гораздо меньше составляющих. Идентификация проводилась до образования в модели (2) искомой статистической биотехнической закономерности максимального количества значимых составляющих.
Удельные ресурсные возможности.
В эту подгруппу факторов производства входят пять экономических величин (табл. 3).
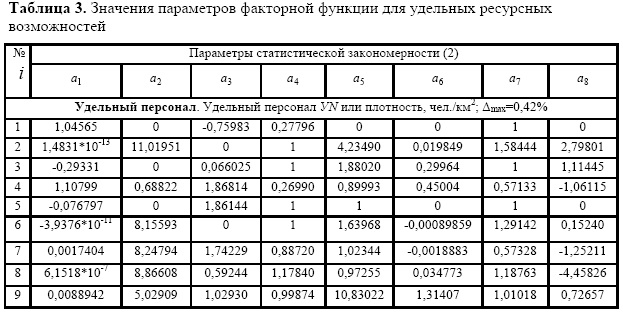
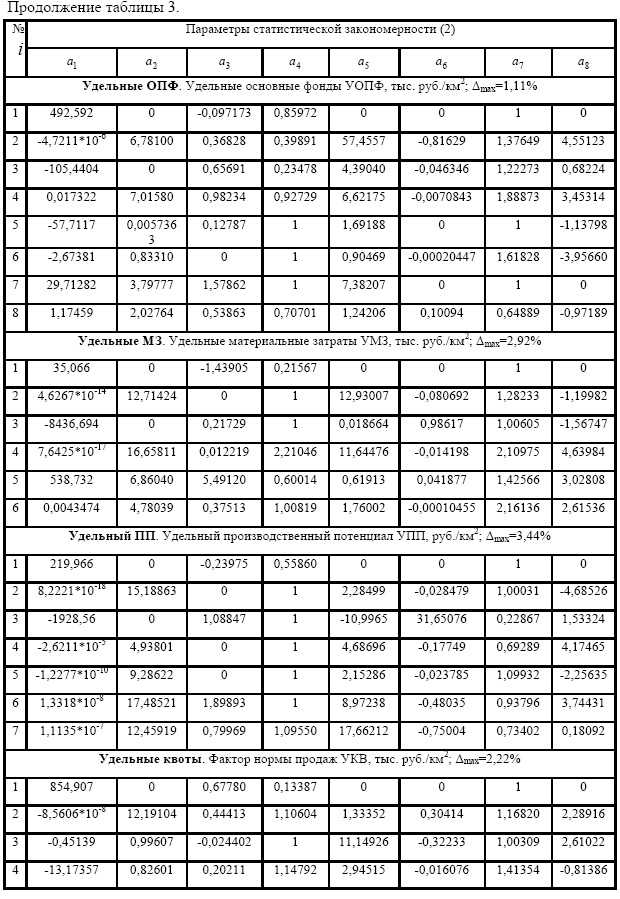
Заметно снижение числа составляющих у фактора УМЗ по сравнению с фактором МЗ (пять cоставляющих вместо 15).
Продукция и удельная продукция сельского района. Результаты деятельности множества сельскохозяйственного
предприятия (табл. 4) в общем случае сводятся не только к производственным показателям. Кроме товарной продукции пока не учитываются косвенные экологические и социальные результаты производства.
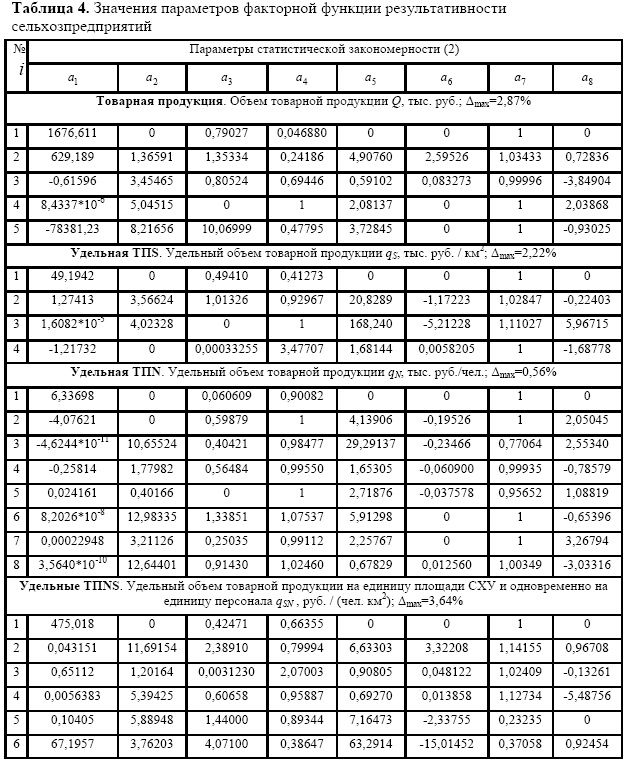
Модель объема товарной продукции имеет всего четыре составляющие. Этот параметр производства сельхозпродукции является контрольным в системе управления сельхозпредприятиями на уровне сельского района.
Поэтому можем сделать вывод о том, что чем меньше количество составляющих в модели, то тем лучше работает подсистема управления сельским хозяйством, в нашем примере на уровне сельского административного района.
Ранговые факторы производства. Эти факторы (табл. 5) являются ранговыми и одновременно кумулятивными по множествам однородных факторов ресурсным возможностям и результатам производства.
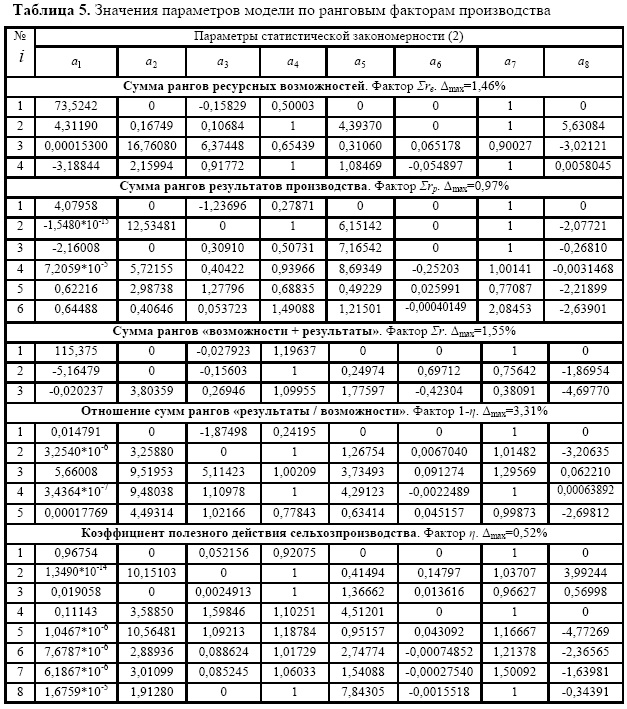
При этом КПД (коэффициент полезного действия) сельхозпредприятия оказывается наиболее точным фактором (0,52 % максимальной относительной ошибки).
Сравнение основных и удельных (по отношению к единице площади СХУ) факторов производства приведено в данных табл. 6.
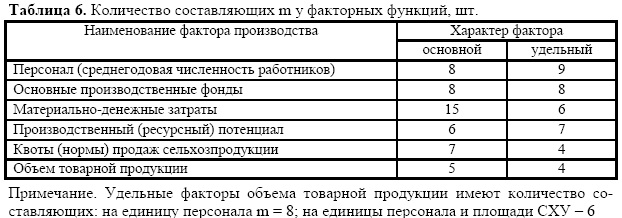
Основные производственные фонды оказались нейтральными к переходу на удельную к площади СХУ величину. Удельные величины по трем факторам (МЗ, КВ и Q) к единице площади сельхозугодий (на 100 га, или все же лучше считать на один км2) дали упрощение моделей.
Результатами производственной деятельности на территории сельского района в ближайшей перспективе могут стать факторы не только товарной продукции, но и другие структурные и функциональные параметры циклической системы обращения производства и потребления. Одним из факторов вполне может стать количество звеньев (принцип: чем меньше, тем лучше) в логистической цепи производства, транспортировки и потребления товарной продукции, а также её видовое разнообразие и др.
В ближайшем будущем возрастет роль факторов адаптивного земледелия, а также выполнения природоохранных и иных экологических мер по достижению территориального экологического равновесия, и на территории России. Поэтому в отдельные подгруппы могут входить социальные и иные факторы, способствующие возрождению села и позволяющие добиться стабильных и устойчивых производственных и иных отношений на селе с р еди людей, а также между людьми и другими видами населения.
СПИСОК ЛИТЕРАТУРЫ:
1. Статистический словарь / Гл. ред. М.А. Королев. Изде 2е, перераб. и доп. М.: Финансы и статистика, 1999. 623 с.
2. Мазуркин, П. М. Математическое моделирование. Идентификация однофакторных статистических закономерностей: Учебное пособие / П.М. Мазуркин, А.С. Филонов. ЙошкарОла: МарГТУ, 2006. 292 с.
3. Мазуркин, П.М. Распределение индекса уровня жизни (по субъектам Российской Федерации): Научное изд. / П.М. Мазуркин. ЙошкарОла: МарГТУ, 2006. 56 с.
4. Мазуркин, П.М. Статистическая эконометрика: Учебное пособие / П.М. Мазуркин. ЙошкарОла: МарГТУ, 2006. 376 с.
5. Шлычков, В.В. Теоретикометодологические аспекты управления ресурсным потенциалом региона / В.В. Шлычков, А.Д. Арзамасцев, Е.П. Фадеева. ЙошкарОла: МарГТУ, 2007. 390 с.
Статья опубликована при поддержке гранта 3.2.3/4603 МОНРФ



