Изучается влияние пленки, покрывающей сферу, на величину силы воздействия набегающего потока и рассматривается следующая модель: твердая сфера радиуса а, покрытая тонкой пленкой толщины h (h/a<<1), которая обтекается стационарным потоком вязкой несжимаемой жидкости, имеющей на бесконечности заданную скорость U = const. Внешняя поверхность пленки деформированная и выписываются граничные условия на поверхности деформированной пленки.
Рассмотрим уравнение движения вязкой жидкости в напряжениях [1]

бесконечности заданную скорость U = const. Внешняя поверхность пленки деформированная и выписываются граничные условия на поверхности деформированной пленки.
Рассмотрим уравнение движения вязкой жидкости в напряжениях [1]
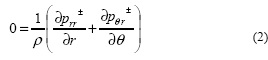
в проекции на тангенциальное направление:
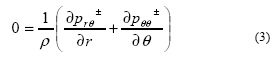
В сферической системе координат уравнение несжимаемости имеет вид:
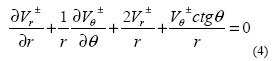
где плюс означает, что мы рассматриваем жидкость как внешнюю среду, а минус означает, что мы рассматриваем среду внутри пленки, покрывающей тело/
Граничные условия имеют вид: 1. на поверхности сферы:
2. на бесконечности:
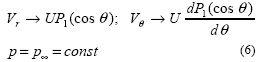
3. на поверхности раздела пленка - набегающий поток выполняется кинематическое условие:
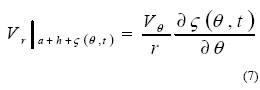
Для постановки граничных условий на границе раздела пленка - набегающий поток, следуя [1] дадим обобщенную формулировку, соответствующую системе уравнений (2-4). Используя принцип виртуальной работы [1] умножим уравнение (2) для внешней среды на вариацию компоненты скорости δV+, уравнение (2) для внутренней среды на вариацию компоненты скорости δV-, уравнение (3) для внешней среды на вариацию компоненты скорости δVθ+, уравнение (3) для внешней среды на вариацию компоненты скорости δVθ-, уравнение неразрывности для внешней среды (4) на δprr+, уравнение неразрывности для внутренней среды (4) на δprr-, кинематическое условие на поверхности раздела пленка - набегающий поток (7) на δpnn , где δpnn - это вариация напряжения, нормального к поверхности раздела. Проинтегрируем полученные уравнения по области Q = R + Q (R - внутренняя среда (пленка), Q - внешняя среда (набегающий поток)). Используем формулу Гаусса - Остроградкого.
Сложим полученные интегральные равенства, проинтегрируем по частям слагаемые, содержащие пространственные производные. Учитывая, что внешняя нормаль к внутренней среде является внутренней нормалью к внешней среде, получим обобщенную формулировку, соответствующую (2-4).
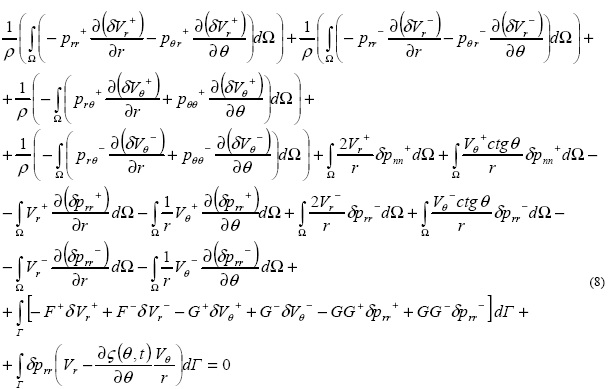
где
![]()
- заданы и определяют на границе раздела пленка - набегающий поток значения функций:
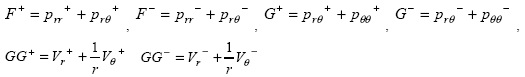
Формула (8) дает обобщенную формулировку краевой задачи. Т.к. на поверхности раздела пленка - набегающий поток не заданы дополнительные поверхностные напряжения (радиальные и тангенциальные), которые могут задаваться как активные силы, например действующие на границе раздела свободная поверхность - воздух, полагаем
![]()
Применение к зависимости (8) теорему Гаусса с целью исключения производных от вариаций и приравнивание к нулю коэффициентов стоящих при независимых вариациях δVθ, δVr, δрrr ,δрnn приводит к уравнениям Навье - Стокса вязкой несжимаемой жидкости, уравнению неразрывности и условиям на границе раздела пленка - набегающий поток:
1. кинематические условия (равенства скоростей):
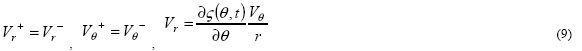
2.динамические условия (равенство нормальных и касательных напряжений):
Последнее равенство является следствием первых двух динамических условий, кинематического условия и уравнения неразрывности. Решая краевую задачу, находим силовое воздействие потока на сферу, покрытую пленкой.
СПИСОК ЛИТЕРАТУРЫ: 1. Коннор Дж. ,Бреббиа К. Метод конечных элементов в механике жидкости. - Л.: Судостроение, 1979, 264 с.



