Scientific journal

Modern high technologies

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

Показано, что формирование структуры дисперсно-наполненных нанокомпозитов на основе фенилона реализуется в евклидовом пространстве, из-за чего величина фрактальной размерности d_f структуры для них не зависит от объемного содержания наполнителя и равна соответствующей величине для матричного полимера. В этом случае величина d_f для полимерных материалов определяется статистической гибкостью полимерной цепи.

Введение дисперсного наполнителя в полимерную матрицу существенно изменяет свойства последней [1]. Этот факт общеизвестен, но возникают определенные затруднения с его количественной оценкой. Для дисперсно-наполненных композитов полигидроксиэфир-графит (ПГЭ-Гр) было обнаружено увеличение фрактальной размерности d_f структуры полимерной матрицы от 2,6 до 2,8 в интервале объемного содержания наполнителя φ_н=0-0,09. Это изменение структуры сопровождается соответствующим повышением механических характеристик композитов (модуля упругости, предела текучести, напряжения разрушения и т.д.) [2]. Указанное изменение структуры композитов ПГЭ-Гр обусловлено ее формированием во фрактальном пространстве, которое создает каркас частиц (агрегатов частиц) наполнителя [3, 4]. Как показали исследования механических свойств нанокомпозитов на основе фенилона, наполненных ультрадисперсными порошками оксинитрида кремний-иттрия и р- сиалона в интервале φ_н=0,001-0,055, для них также наблюдается некоторое повышение механических характеристик (в пределах 10 %), причем величины модуля упругости Е и предела текучести σ_T увеличиваются пропорционально [5]. Авторы [5] показали, что указанное увеличение Е и σ_T реализуется за счет формирования межфазных областей и собственно наполнителя, если структура полимерной матрицы формируется в евклидовом пространстве (d_f не зависит от φ_н). Поэтому целью настоящей работы является более подробное исследование формирования структуры указанных нанокомпозитов на основе фенилона.

Исследовали полимерные нанокомпозиты на основе термостойкого ароматического полиамида фенилон С-2. В качестве наполнителя использовали ультрадисперсные порошки оксинитрида кремний-иттрия и β-сиалона (твердый раствор Al₂O₃ и AlN в b-Si₃N₄). Диаметр частиц наполнителя составлял 64 и 80 нм, удельная поверхность 43 и 60 м²/г, соответственно, и плотность 1820 кг/м³.

Введение наполнителя в полимерную матрицу осуществляли во вращающемся электромагнитном поле с помощью неравноосных ферромагнитных частиц. Отношение длина/диаметр этих частиц составляло 4-5, объем загруженных в реактор аппарата частиц был в пределах 0,040,05 от объема действия электромагнитного поля, величина электромагнитной индукции вращающегося поля - в пределах 0,08-0,12 Тл. При указанных параметрах экспериментально обнаружено, что оптимальная продолжительность обработки нанокомпозитов в электромагнитном поле составляет 270-300 с. Приготовление образцов осуществляли методом компрессионного прессования при температуре 537-616 К и давлении 40-100 МПа.

Определение механических свойств в испытаниях на сжятие выполнено на испытательной машине FPZ-100/1 фирмы HECKERT (ГОСТ 4651-78) при температуре 293 К и скорости деформации 10^-3с^-1.

Как известно [6], величину фрактальной размерности d_f структуры композита можно определить следующим образом:

d_f = (d - 1)(1 + v),    (1)

где d - размерность евклидова пространства, в котором рассматривается фрактал (очевидно, в нашем случае d=3), v - коэффициент Пуассона, оцениваемый с помощью уравнения [7]:

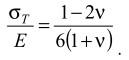 (2)

На рис. 1 приведена зависимость рассчитанной указанным образом размерности d_f от объемного содержания наполнителя φ_н для исследуемых нанокомпозитов. Как следует из данных этого рисунка, выполняется условие d_f=const в пределах 3 %-го отклонения и, что наиболее важно, величины d_f для исходного матричного фенилона и нанокомпозитов равны.

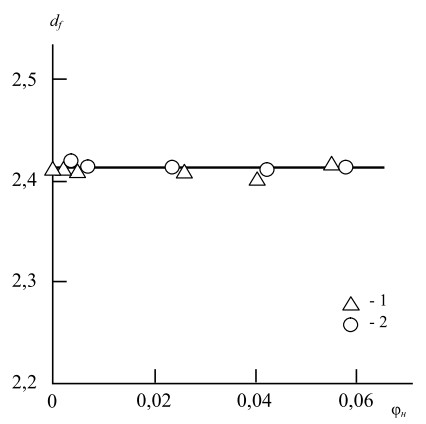
Рисунок 1. Зависимость фрактальной размерности структуры d_f  от объемного содержания наполнителя φ_н  для нанокомпозитов на основе фенилона, наполненных оксинитридом кремний-иттрия (1) 
и β-сиалоном (2).

Поскольку в исходном фенилоне нет фактора (наполнителя), изменяющего размерность пространства, в котором формируется структура, и d=3, то и для нанокомпозитов должно выполняться это условие, т.е., формирование их структуры реализуется в трехмерном евклидовом пространстве. Как известно [8], в этом случае показатель Флори v_F связан с размерностью евклидова пространства d следующим простым соотношением:

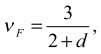             (3)

что для d=3 дает v_F=0,6.

В свою очередь, между d_f и v_F существует следующая взаимосвязь [6]:

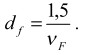
Таким образом, для d=3 и v_F=0,6 величина d_f всегда равна 2,50. Этот расчет подтверждается компьютерным моделированием траектории случайного блуждания, т.е., траектории точки. Однако в случае структуры полимеров статистические сегменты объединены в полимерную цепь, что существенно отличает их от точечного объекта, совершающего случайное блуждание. В этом случае величина d_f определяется гибкостью полимерной цепи, которую можно описать характеристическим отношением С_∞, следующим образом [6]:

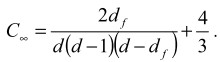                (5)

Для фенилона величину С_∞ можно оценить из следующего эмпирического уравнения [6]:

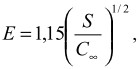
где S - площадь поперечного сечения макромолекулы, равная 17,6  для фенилона, а величина Е дается в ГПа.

Из уравнения (6) получим С_∞=2,85 при Е=2,857 ГПа в испытаниях на сжатие, и из уравнения (5) - d_f=2,46, что близко к оценке согласно уравнению (1) (см. рис. 1).

Таким образом, результаты настоящей работы предполагают формирование структуры дисперсно-наполненных нанокомпозитов на основе фенилона в евклидовом пространстве, из-за чего величина d_f для них не зависит от объемного содержания наполнителя (по крайней мере, в интервале 0-0,055) и равна соответствующей величине для матричного полимера. В этом случае величина d_f для полимерных материалов определяется статистической гибкостью полимерной цепи.

СПИСОК ЛИТЕРАТУРЫ

1. Липатов Ю.С. Физико-химические основы наполнения полимеров. М., Химия. 1991. 259 с.
2. Новиков В.У., Козлов Г.В. // Механика композитных материалов. 1999. Т. 35. № 3. С. 269.
3. Козлов Г.В., Яновский Ю.Г., Липатов Ю.С. // Механика композиционных материалов и конструкций. 2002. Т. 8. № 4. С. 467.
4. Козлов Г.В., Липатов Ю.С. // Механика композитных материалов. 2004. Т. 40. № 6. С. 827.
5. Козлов Г.В., Буря А.И., Алоев В.З., Гринева Л.Г. // В сб.: Механика и процессы управления. Т. 1. Екатеринбург. 2004. С. 97.
6. Kozlov G.V., Zaikov G.E. Structure of the Polymer Amorphous State. Utrecht-Boston, Brill Academic Publishers. 2004. 465 p.
7. Козлов Г.В., Сандитов Д.С. Ангармонические эффекты и физико-механические свойства полимеров. Новосибирск, Наука. 1994. 261 с.
8. Aharony A., Harris A.B. // J. Stat. Phys. 1989. V. 54. № 3/4. P. 1091.