Многие измеряемые физические процессы могут рассматриваться как выходные сигналы линейных динамических систем (ЛДС) при подаче на вход стационарных случайных воздействий (ССВ) с ограниченной мощностью (дисперсией). Особый интерес представляет переходный режим от скачкообразного изменения амплитуды реализации ССВ в границах динамического диапазона. В этом случае выходной сигнал ЛДС является нестационарным сигналом, статистические характеристики которого асимптотически устремятся к новым установившимся значениям. При этом возможны значительные кратковременные расширения границ динамического диапазона (выбросы дисперсии) сигнала и его производной относительно нового установившегося значения.
Скачкообразный характер изменения воздействия близок к ударным нагрузкам. В этом смысле реакция ЛДС в переходном (неустановившемся) режиме может приближаться к экстремальной и служить оценкой сверху для взаимодействия ЛДС с нестационарным воздействием, параметры которого плавно изменяются в тех же границах. К тому же в рамках этой модели проще и удобнее более обоснованно определить априорные ограничения: с одной стороны - это динамические свойства ЛДС, с другой - динамический диапазон ССВ.
В задачах измерения и обработки подобных сигналов игнорирование выбросов и учет только установившихся значений статистических характеристик может привести к занижению частоты дискретизации цифровых алгоритмов, а в конечном итоге к значительному росту погрешности измерения/обработки. Однако выбросы в переходных режимах могут появляться не всегда, а лишь при определенных сочетаниях параметров ССВ и ЛДС.
Известно общее решение для определения корреляционной функции асимптотического нестационарного выходного сигнала ЛДС при скачке амплитуды реализации ССВ от 0 до текущего значения:
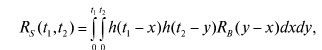
где h - импульсная характеристика ЛДС; RB - автокорреляционная функция ССВ.
Производная nго порядка реакции ЛДС характеризуется корреляционной функцией:
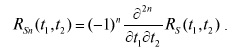
Соответствующие дисперсии имеют вид:
На практике наибольший интерес представляет закон изменения во времени дисперсии
первой производной 
, который определяет закон
изменения текущей частоты дискретизации сигнала ЛДС.
Возможны следующие способы скачкообразного изменения амплитуды в границах динамического диапазона ССВ:
-от 0 до произвольного значения (переходный режим 1го вида);
-от произвольного значения до 0 (переходный режим 2го вида);
-от произвольного значения до противоположного по знаку аналогичного значения (инверсия знака) (переходный режим 3го вида).
Теоретические модели дисперсии первой производной асимптотически нестационарных сигналов во всех представленных переходных режимах рассмотрены в [1].
Для экспериментальной проверки теоретической модели разработана программа имитационного моделирования на языке Delphi. Исходными данными являются: вид и параметры ССВ и ЛДС; вид переходного режима; длина интервала времени; число реализаций. Экспериментальные значения дисперсии 1й производной реакции ЛДС вычисляется путем усреднения по ансамблю реализаций. После завершения моделирования на экране отображается график экспериментальных значений дисперсии первой производной с наложенным на нее в едином масштабе графиком теоретических значений дисперсии первой производной, вычисленных по расчетным формулам. Полученные графики могут быть сохранены в графическом формате bmp.
Вывод:
1. Результаты моделирования подтверждают правильность расчетных формул дисперсии первой производной асимптотически нестационарных сигналов типа переходный режим.
Список литературы
1. Мадыев А.П., Ширапов Д.Ш. Определение дисперсии первой производной асимптотически нестационарных сигналов типа переходный режим и анализ ее общих свойств // Современные технологии. Системный анализ. Моделирование. ИрГУПС. - 2008.- №1- С. 106109.