Для этой колонки сам «числовой полоз» (на рис. 1 показан жирной линией) «числовых санок» образован степенями числа 3 (3n, где n - натуральное число), причём длина полоза бесконечна. В активных точках «числового полоза», т.е. в тех местах где расположены степени числа 3 (на рисунке отмечены красными точками), к нему прикреплены числовые ленточки, причём числа, формируемые на разных числовых ленточках, друг с другом не перекрываются. Т.е. каждая числовая ленточка содержит непересекающееся с другими подмножество чисел данной колонки, порождающими элементами которых служат те или иные степени числа 3 (3n). Верх (верхнюю плоскость) «числовых санок» для данного полоза образует самая верхняя ленточка, идущая от элемента 3 (31). Это число одновременно являющегося и образующим элементом «числового полоза». Если объединить все подмножества чисел, принадлежащих каждой числовой ленточке, то они все вместе сформируют колонку симметрии числа 3 относительно F-оси, как это показано в работе [2] и на рис. 2 этой работы стрелками. Тем самым произойдёт формирование, т.е. заполнение числами без пропусков и повторов (наложений друг на друга), всех число-мест колонки 3 «числовых санок».
Аналогичные «числовые полозья» формируют и числа 2 (22n-1 - нечётные степени числа 2) и 4 (22n - чётные степени числа 2), но при этом числовые ленточки от активных точек этих полозьев переплетаются между колонками 2 и 4. При этом сохраняются все выше перечисленные свойства, что и для колонки 3, только теперь совместный результат распределён между двумя колонками - 2 и 4. В этом случае ко-лонки 2 и 4 можно считать комплементарными. Получается своеобразное спутанное состояние ленточек, но полозья чётко распределены между колонками.
Для колонок 1 и 5, в которых расположены все простые числа и все из произведения, аналогию можно продолжить. При этом сохраняются все указанные выше свойства, но здесь возникает (добавляется) новое свойство. «Числовых полозьев» под каждой из этих колонок много, они как бы вложены друг в друга и их образующими являются степени всех простых чисел, находящихся в этих колонках (Fn, где F - любое простое число, n - любое натуральное число). Причём каждое простое число образуют свой индивидуальный «числовой полоз». Ленточки от активных точек полозьев так же имеют место быть, и переплетены между колонками 1 и 5, т.е. колонки 1 и 5 образуют комплементарную пару.
Есть и ещё одна особенность. «Числовые полозья» пятой колонки, в отличие от всех ранее рассмотренных полозьев, которые всегда лежат в плоскости, проходящей через ту колонку, откуда у них взята образующая, изогнуты. Т.е. активные точки полозьев с образующими из колонки 5 через раз то расположены в колонке 1, то в колонке 5, откуда у них и начинаются цифровые ленточки. Таким образом количество цифровых ленточек, начинающихся в колонке 1 в три раза больше, чем количество цифровых ленточек, начинающихся в колонке 5. Но поскольку ленточки переплетаются между колонками 1 и 5, то это не сказывается на плотности чисел, которые они представляют для каждой из колонок.
Есть ещё один особый полоз, который формируется первым элементом первой колонки. Это «числовой полоз», образующей которого служит число 1, и который имеет нульмерную длину. Отметим, что полозья в колонках симметрий (колонки 2, 3, 4) имеют бесконечную длину, а полозья в колонках 1 и 5 (колонки расположения простых чисел) - бесконечно-мерную длину.
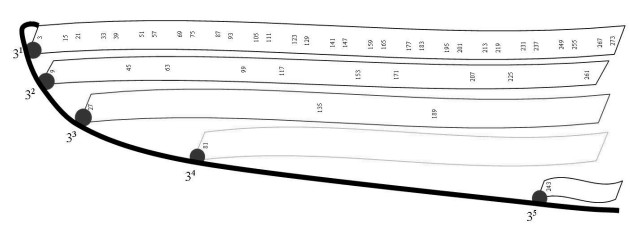
Рис. 1
Поскольку на плоскости отобразить вложенные друг в друга «числовые полозья» для колонок 1 и 5 затруднительно, т.к. внутри любого произвольно взятого «числового полоза» должно быть размещено бесконечно большое число вложенных в него других «числовых полозьев», образованных бесконечно большим числом простых чисел, больших исходного и служащих образующими для данных «числовых полозьев», то перейдём к центральной проекции. Причём в качестве таковой выберем обратную перспективную проекцию, т.е. такую, в которой точка схода (бесконечно удалённая точка проективного преобразования) расположена в центре, а все исходящие из неё лучи расходятся на бесконечности. В этом случае между любыми бесконечно близко расположенные друг к другу «числовыми полозьями-лучами» можно вместить бесконечно много других «числовых полозьев», т.к. все «полозья-лучи» расходятся между собой на бесконечности, тем самым постоянно освобождают место для размещения новых (вновь возникающих) «числовых лучей-полозьев».
Поскольку верх «числовых санок» образован шестью колонками, то для размещения «числовых полозьев» нам достаточно шести секторов. Поэтому в качестве основы построения выберем шестиугольник. Отметим, что шестиугольник, как геометрическая фигура, образуется естественным образом, т.к. его сторона равна радиусу окружности, на которой он строится [3]. Таким образом, построение этой фигуры не зависит от принятых единиц измерения, теоретических расчётов и обобщений, набора аксиом и правил оперирования ими, вводимых человеком в результате его мыслительной деятельности, произведённой относительно окружающего его мира (потока событий внешней среды), в том числе и на прежних этапах своего развития. Такое построение дано нам естественным природным образом, не требующим такого либо предварительного знания (т.е. без этапа сворачивания информации о внешней среде).
На рис. 2 показан пример построения таких секторов в районе точке проецирования, которая совпадает с центром вспомогательной окружности, на которой, как на образующей, и строятся сектора. На рисунке точка проецирования расположена в центре, границы секторов показаны тонкими линиями, «числовые полозья» - толстыми линиями. В начале каждого полоза стоит кружочек и указанием числа, являющегося образующим для данного «числового полоза». Длины секторов и длины полозьев бесконечны, поэтому их концы показаны пунктирной линией.
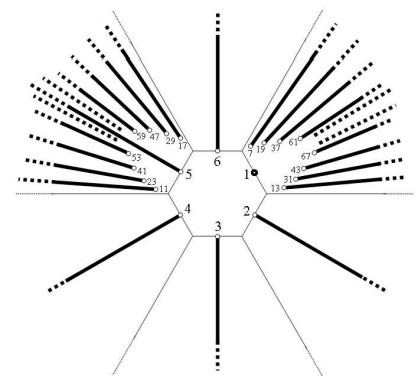
Рис. 2
В каждом из секторов 2, 3, 4 будет только по одному лучу, под которыми (в плоскости оси Z, перпендикулярной рисунку) скрывается по единственному «числовому полозу», аналогичному приведённому на рис. 1, со всеми их «числовыми ленточками». В секторе 6 отсутствует полоз и идёт «сшивка» рядов «поленницы» между собой. Это зона своеобразной «застёжки-молнии» между рядами «поленницы» [1] свёрнутыми в кольца. При сдвиге колец в месте стыка на половину шага образуется непрерывная раскручивающаяся спираль натурального ряда чисел.
Иная картина в секторах 1 и 5. В них множество лучей, каждый из которых начинается в точке, эквивалентной простому числу и далее распространяется до бесконечности, образуя под каждым из них (лучей) свой «числовой полоз». Все простые числа лежат на различном удалении от центра проецирования. Тем самым количество «числовых полозьев-лучей», которые образованы этими числами и которые могут быть размещены в данном секторе с удалением от его центральной точки, стремиться к бесконечности, и все они лежат по обе стороны центрального луча в секторе 5 и отсутствующего центрального луча в секторе 1. Центральный луч в секторе 1 представлен единственной точкой, причём ближайшей к центру проецирования.
Масштаб расположения «числовых полозьев-лучей» на рис. 2 не соблюдается, что сделано для большей наглядности рисунка. В линейной метрике плотность расположения «числовых полозьев-лучей» вокруг центрального луча не увеличивается с расстоянием. Все ранее возникшие «числовые полозья-лучи» расположены дальше от центрального луча, чем те, что только что появились. Т.е. каждый вновь возникший «числовой полоз-луч» всегда ближе к центральному, чем все уже существующие.
Таким образом ряд натуральных чисел (линейная, вернее последовательная цепочечная структура) может быть представлен в виде объемного тела - «числовых санок», у которых: верхней поверхностью служат основные числовые ленточки от всех простых чисел и чисел симметрии F-оси плюс колонка периода (циклического числа 6); «числовые полозья» образованы нечётными и чётными степенями чисел 2, степенями чисел 3 и степенями всех простых чисел из 1 и 5 колонок; в активных местах к «числовым полозьям» прикреплены числовые ленточки, которые перевиваются между комплементарными колонками, не затрагивая и не влияя при этом на другие колонки.
Сейчас зима и катаясь с горок на санках, не забывайте про существование «числовых санок», которые по аналогии с обычными санями могут привести Вас к внутреннему устройству натурального ряда чисел и подсказать место простых чисел в этой структуре.
ЛИТЕРАТУРА
- Тупик Н. В. Являются ли простыми числа 2 и 3 //"Успехи современного естествознания", М.: РАЕ, 2008, № 8, с.86 - 88.
- Тупик Н. В. Симметрии F-оси //"Современные наукоёмкие технологии", М.: РАЕ, 2008, № 9, с.45 - 47.
- Правильные шестиугольники // Википедия - свободная энциклопедия, 2008 [http:// ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%B0% D0%B2%D0%B8%D0%BB%D1%8C%D0%BD% D1%8B%D0%B9_%D1%88%D0%B5%D1%81% D1%82%D0%B8%D1%83%D0%B3%D0%BE% D0%BB%D1%8C%D0%BD%D0%B8%D0%BA].



