Как известно [1], в тонкопленочной (толщина пленки h соизмерима с длиной акустической волны X) пьезокристаллической структуре возможно распространение электроакустических волн, называемых волнами Лэмба. Волны Лэмба, как и поверхностные акустические волны (ПАВ), могут возбуждаться при помощи встречноштыревых преобразователей (ВШП) либо однофазных преобразователей (ОП), нанесенных на поверхность тонкопленочной пьезоструктуры [1]. Рабочая частота этих волн определяется скоростью (V) волны и пространственным периодом (Р) преобразователей (ВШП, ОП), возбуждающих волну. При фиксированной толщине пленки могут существовать несколько вариантов (мод) волн Лэмба, отличающихся скоростью (V) волны и коэффициентом электромеханической связи (K2). Как известно, одной из перспективных пьезоструктур является нитрид алюминия (AlN) [2]. Скорости высокоскоростных мод Лэмба в A1N могут иметь значения (~10 км/с), существенно большие, чем скорость ПАВ в соответствующей полубесконечной среде A1N (~5,4 км/с), что дает возможность использовать высокоскоростные моды Лэмба для разработки различных СВЧ акустоэлектронных компонент в диапазоне рабочих частот вплоть до нескольких ГГц [3].
Важным требованием к пьезоматериалам, применяемых на практике, относится их термостабильность [1]. Пьезокристалл нитрида алюминия по своим термостабильным свойствам уступает традиционно используемым на практике термостабильному пьезокварцу [2]. Нанесение на поверхность пьезокристаллической подложки слоев из других материалов в некоторых случаях позволяет улучшить параметры распространяющейся электроакустической волны. Например, с помощью материала одного слоя определенной толщины, нанесенного на поверхность пьезокристаллической подложки, изначально не обладающей термостабильными свойствами, можно термокомпенсировать акустическую волну [1].
Целью работы является теоретический расчет и анализ параметров электроакустических волн Лэмба, распространяющихся в тонкопленочных пьезоструктурах из (0001) A1N и в двойных тонкопленочных структурах (0001)AlN/SiO2 (аморфный оксид кремния), которые могут быть использованы для термостабилизации тонкопленочных СВЧ акустоэлектронных устройств на основе A1N.
1. Симметричные и антисимметричные моды Лэмба в тонкопленочной структуре AlN
Волны Лэмба делятся на две группы: симметричные (s) и антисимметричные (a) [4]. На рис. 1. показаны картины механических смещений частиц среды для нулевой симметричной (рис. 1,а) и антисимметричной (рис. 1,б) моды Лэмба. В симметричных волнах движение происходит симметрично относительно плоскости Z = 0, т.е. в верхней и нижней половинах пластины механическое смещение ux имеет одинаковые знаки, а u противоположные. В антисимметричных волнах движение антисимметрично относительно плоскости Z = 0, т.е. в верхней и нижней половинах пластины механическое смещение ux имеет противоположные знаки, а u одинаковые.

а
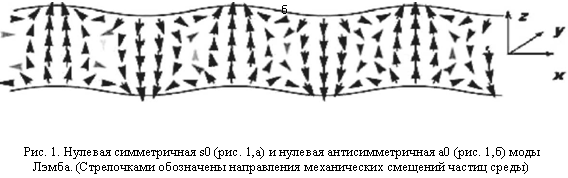
Для изучения свойств электроакустических волн Лэмба, распространяющихся в тонкопленочных пьезоструктурах, необходимо воспользоваться волновыми уравнениями пьезоакустики [1]:
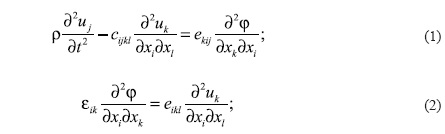
здесь ui - смещение вдоль декартовой координаты Xj; t - время; r плотность материала; j электрический потенциал; Сijkl, ekij, eik тензоры упругих, пьезоэлектрических и диэлектрических констант материала в рабочей декартовой системе координат; i, j, k, l = 1, 2, 3.
Обычно плоскость (срез) пьезокристалла и направление распространения акустической волны задается при помощи трех углов Эйлера (φ, θ, ψ), первые два из ко торых (φ, θ) определяют срез (плоскость), а третий угол (ψ) определяет конкретное направление распространения [1]. Ориентацию в пьезокристалле можно также задавать при помощи индексов Миллера (i j к l).
Решение уравнений (1), (2) может быть осуществлено только численным способом, используя например, методику Фартры: коэффициент электромеханической неллаДжонса [1]. Воспользовавшись Воспользовавшись соответствующими граничными условиями, вычисляется фазовая скорость (V) волны, далее рассчитываются основные параметры: коэффициент электромеханической связи (K2), температурный коэффициент задержки (ТКЗ), угол потока энергии (УПЭ), араметр анизотропии (γ) и т.д.) электроакустических волн [1, 5]:
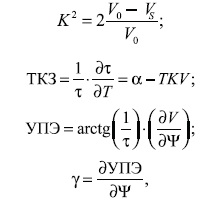
где V0 и VS фазовые скорости волны на открытой и металлизированной поверхностях кристалла; т время задержки; Т температура; TKV = (l/v(∂V/∂T)) температурный коэффициент скорости; α - коэффициент линейного расширения материала в направлении распространения волны;ψ- третий угол Эйлера.
Как известно, тонкопленочная гетероэптитаксиальная ориентированная пьезокристаллическая структура (0001) A1N может быть выращена на подложке из кремния (111)Si различными методами: реактивного магнетронного распыления, газофазной эпитаксии, газофазной эпитаксии из металлоорганических соединений и молекулярнолучевой эпитаксии.
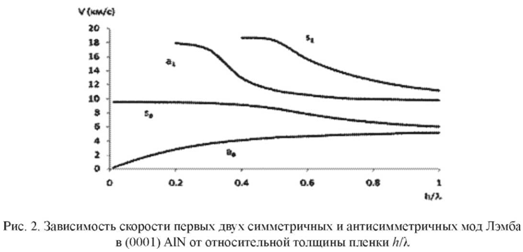
На рис. 2 показаны рассчитанные с помощью собственного программного обеспечения [5, 6] скорости симметричных и антисимметричных мод Лэмба в тонкопленочной структуре (0001) A1N в зависимости от относительной толщины пленки h/λ (h толщина пленки). Из рис. 2 видно, что скорость V мод Лэмба имеет дисперсию (зависит от относительной толщины пленки). Нулевая симметричная мода Лэмба S0 при малой толщине пленки имеет скорость порядка ~ 10 км/с, а скорости высокоскоростных мод a s1 могут иметь значения порядка ~ 18 км/с.
На рис. 3 показаны рассчитанные зависимости К2 и ТКЗ для симметричной моды s0 в пленке (0001)AlN от относительной толщины пленки h/k. Как видно из рис. 3, коэффициент электромеханической связи К2 для моды S0 максимален при относительной толщине пленки hfk = 0,5 и имеет величину ~ 1,6 %, что существенно выше величины К2ПАВ ~ 0,28 % для ПАВ в полубесконечной подложке AlN Zсреза (углы Эйлера ф = 0°,9 = 0°, 4 = 0° 360°). Заметим, что поскольку кристаллический AlN относится к гексагональному типу симметрии класса 6 mm, параметры акустической волны в плоскости Zсреза одинаковы (не зависят от угла 4). Рассчитанная величина ТКЗ симметричной нулевой моды S0 в пленке (0001) AlN лежит в пределах (2530)х106/°С и имеет минимальное значение также при h/k = 0,5, что сравнимо с ТКЗ для ПАВ в AlN Zсреза.
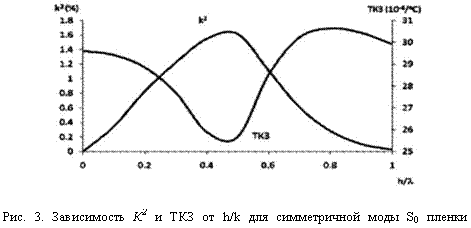
Таким образом, волны Лэмба, распространяющиеся в пленке (0001)AlN могут быть использованы при конструировании различных СВЧ акустоэлектронных устройств резонаторов, фильтров, линий задержки с целью повышения рабочей частоты.
2. Электроакустические волны Лэмба в тонкопленочной двухслойной структуре AlN/SiO2
Одной из основных проблем всех акустоэлектронных устройств является их термостабильность. Как видно из рис. 3, волны Лэмба в пленке (0001) AlN не являются термостабильными. Это обусловлено отрицательными значениями температурных коэффициентов констант упругости AlN [7]. Для компенсации этого эффекта может быть использована структура из двух тонких пленок AlN и любого материала с положительными температурными коэффициентами констант упругости, т.е. с отрицательным ТКЗ. В частности, таким свойством обладает пленка аморфного оксида кремния Si02 [8].
Для анализа параметров волны в двухслойной тонкопленочной структуре (0001) AlN/(аморфный) SiO2 необходимо одновременно решить волновые уравнения (1), (2) в двух средах с соответствующими граничными условиями по методике, описанной в [6, 9]. На рис. 4 показаны рассчитанные зависимости V и K2 в структуре (0001)AlN (h/λ = 0,2)/аморфный Si02 для нулевой симметричной моды Лэмба S0 от относительной толщины пленки Si02 (h2/λ).
Из рис. 4. видно, что скорость волны в двухслойной тонкопленочной структуре (0001)AlN/SiO2 уменьшается с ростом относительной толщины пленки h2/λ Si02. Это связано с тем, что в данном случае энергия волны сосредоточена в двух материалах и обобщенная скорость волны определяется упругими свойствами этих материалов. Скорость акустической волны в Si02 меньше, чем в (0001)AlN, поэтому с ростом толщины пленки Si02 обобщенная скорость в системе уменьшается. На рис. 5 показана расчетная зависимость ТКЗ в структуре (0001)AlN (h/k = 0,2)/SiO2 от относительной толщины h2/λ пленки SiO2 при относительной толщине пленки (0001) AlN h/λ = 0,2. Из рис. 5 видно, что в данном случае термокоменсация (ТКЗ = 0) акустической волны имеет место при h2/λ ~ 0,1. Таким образом, для термокомпенсации (ТКЗ ~ 0) нулевой симметричной моды Лэмба S распространяющейся в пленке (0001)AlN с относительной толщиной h/λ = 0,2, необходимо нанести на нее пленку SiO2, относительная толщина которой в два раза меньше h2/λ ~ 0,1.
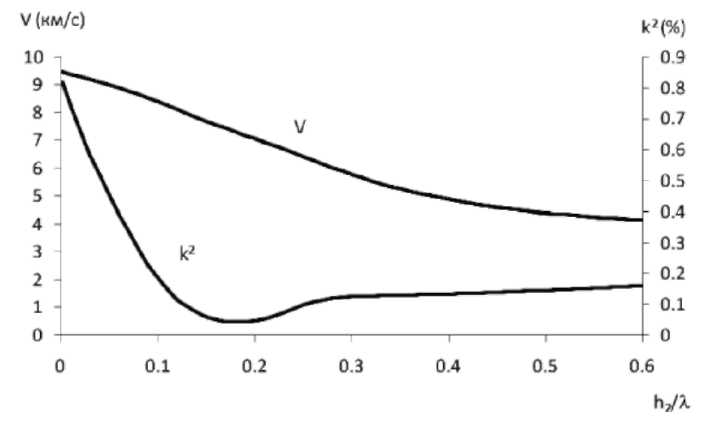
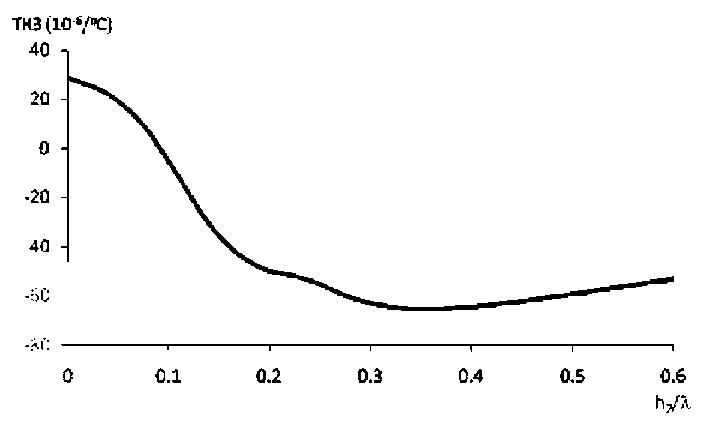
Рис. 5. Зависимость ТКЗ симметричной моды Лэмба S0 в двухслойной тонкопленочной структуре (0001)AlN/SiO2 от относительной толщины h2/λ пленки SiO2 при относительной толщине пленки (0001)AlN - h/λ = 0,2
Во всех расчетах материальные константы материалов AlN, SiO2 были взяты из работ [7, 8].
3. Акустоэлектронный СВЧ резонатор
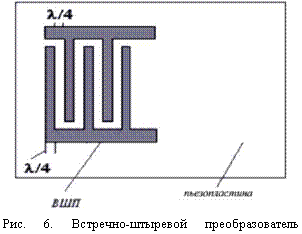
Конструктивно, тонкопленочный акустоэлектроный СВЧ резонатор состоит из пьезокристалической структуры, с нанесенной на ее поверхность методом фотолитографии ВШП, служащего для приема и возбуждения волны. ВШП представляет из себя систему периодических вложенных друг в друга металлических электродов с периодом Р = λ/2 (рис. 6) [1]. При изготовлении акустоэлектронного резонатора, на верхней поверхности пьезопластины методом фотолитографии формируется ВШП. Рабочая резонансная частота резонатора F = V/λ = V/2Р, определяется скоростью (V) волны и пространственным периодом (Р) электродов ВШП. Ширина металлических электродов ВШП и зазор между ними l/4. Тогда на рабочей частоте резонатора F = 5 ГГц, работающего на нулевой симметричной моде Лэмба S0 (V ~ 10 км/с) период электродов Р = λs0/2 = 1 мкм, ширина электродов ВШП и зазор между ними ~ 0,5 мкм, что приемлемо для предельной точности фотолитографии при изготовлении ВШП (~ 0,5 мкм) на обычных фотолитографических установках.
Возбуждение волны Лэмба возможно также при помощи однофазного преобразователя (ОП) [1].
На рис. 7 показана конструкция однофазного преобразователя, электроды которого расположены на обеих сторонах поверхности пьезопластины. При этом нижний электрод сплошной, а ширина верхних периодических электродов и зазор между ними равны 1/2.
Использование ОП дает возможность повысить рабочую частоту такого резонатора в 2 раза (F = 10 ГГц) при той же предельной точности фотолитографии (~ 0,5 мкм).
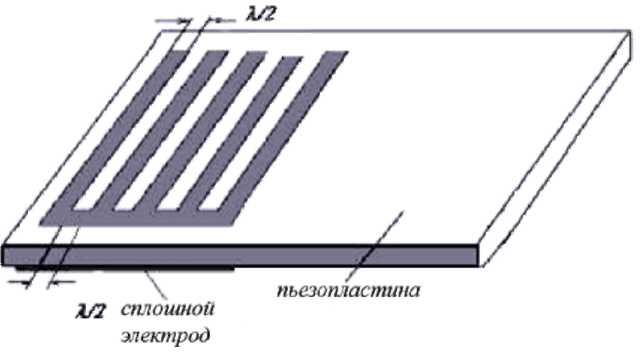
На рис. 8 показан один из вариантов реализации тонкопленочного СВЧ акустоэлектронного резонатора на нитриде алюминия, использующего волны Лэмба.
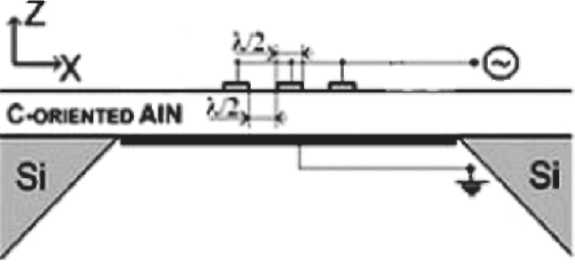
Рис. 8. Структурная схема СВЧ
акустоэлектронного резонатора на волнах Лэмба
Методом газофазной эпитаксии или другим на подложке (111)Si может быть выращена ориентированная гетероэпитаксиальная структура (0001)A1N [10]. Путем глубокого травления подложки кремния можно сформировать рабочую зону СВЧ резонатора, представляющего собой мембрану (тонкую пленку A1N), на которой будет сформирован однофазный преобразователь для возбуждения акустической волны. Для термокомпенсации акустоэлектронного резонатора методом магнетронного напыления может быть нанесена пленка SiO2. Рабочая частота термокомпенсированного акустоэлектронного резонатора F = V/λ ~ 9 ГГц (Х = 1 мкм) при толщинах пленки A1N h = 0,2 мкм, пленки SiO2, h2 = 0,1 мкм.
Заключение
Показано, что волны Лэмба, распространяющиеся в тонких ориентированных пленках (0001)A1N/SiO2 могут быть использованы при конструировании термокомпенсированных акустоэлектронных устройств СВЧ диапазона. Высокая скорость волн Лэмба обеспечивает возможность продвижения в область более высоких частот (110 ГГц), чем для обычных ПАВ устройств (до 1 ГГц). Рассчитаны конкретные соотношения толщин пленок (0001)A1N и SiO2, при которых возможна термокомпенсация СВЧ акустоэлектронного резонатора, работающего на нулевой симметричной моде Лэмба.
СПИСОК ЛИТЕРАТУРЫ
1. У. Мэзон, Р. Терстон, Физическая акустика. Принципы и методы. М.: Мир, 1973. 432 с.
2. ChiaChi Sung, YuanFeng Chiang, Theoretical Analysis of SAW Propagation Characteristics in (100) Oriented AlN/Diamond Structure // IEEE Ultrason. Symp. 2009.P. 446449.
3. Matteo Rinaldi, Chiara Zuniga, Chengjie Zuo and Gianluca Piazza, AlN ContourMode Resonators for NarrowBand Filters above 3 GHz // IEEE Ultrason. Symp. 2009. P. 7074.
4. И.А. Викторов, Звуковые поверхностные волны в твердых телах. М.: Наука, 1981. 287 с.
5. Двоешерстов М.Ю., Чередник В.И., Электроакустические волны Лэмба в пьезокристаллических пластинах // Акустический журнал. 2004. Т. 50, №4. С. 16.
6. Dvoesherstov M.Yu., Cherednick V.I., Bhattacharjee K. Plate and Gap Acoustic Waves for Highly Sensitive Gas and Liquid Sensors // IEEE Ultrason. Symp. 2004. Р. 15531556.
7. Tsubouchi K., SugaI K., Mikoshiba N., A1N Material constants evaluation and saw properties on A1N/A12O3 and A l N / S i //IEEE Ultrason. Symp. 1981. P. 375380.
8. Bjurstrom J., Wingqvist G., Yantchev V., Katardjiev I. Temperature compensation of liquid FBAR sensors // J. Micromech. Microeng. 2007. Vol. 17. P. 651658.
9. Чередник В.И., Двоешерстов М.Ю. Численный расчет параметров поверхностных и псевдоповерхностных акустических волн в многослойных структурах // Журнал технической физики. 2003. Т. 73, Вып. 10. С. 106112.
10. Tsubouchi K., Mikoshiba N. Zero temperature coefficient saw delay line on A1N epitaxial films // IEEE Ultrason. Symp. 1983 P. 299310.



