Из закона инерции Галилея (I закон Ньютона) следует, что всякое тело оказывает сопротивление
при попытках привести его в движение или изменить модуль или НАПРАВЛЕНИЕ его скорости. Это свойство тел называется
инертностью. Чтобы преодолеть сопротивление, необходимо приложить усилие, т.е. совершить работу.
Формула для вычисления работы изменения скорости тела приведена во всех
учебниках физики. Она получена на основе II закона Ньютона для результирующей силы
![]() в виде
в виде
![]() (1)
(1)
Поскольку путь
![]() , то работу можно выразить через импульс силы
, то работу можно выразить через импульс силы
![]()
![]() (2)
(2)
Определим работу, которую нужно затратить, чтобы изменить
НАПРАВЛЕНИЕ движения тела, т.е. повернуть вектор скорости V0
на некоторый
угол α
. Автор [1-3] назвал её РАБОТОЙ ПОВОРОТА. При
изменении направления движения при
V0=const кинетическая
энергия тела не изменяется, но работа должна быть затрачена, так как тело
оказывает сопротивление к попытке изменить направление его скорости. Изменение
направления движения будем производить за счет действия МГНОВЕННОЙ СИЛЫ
F2, для чего устремим интервал действия силы
t→0, а величину силы F→∞
. Тогда получим мгновенную силу в виде
![]() , где
, где ![]() - дельта-функция
Дирака [4].
- дельта-функция
Дирака [4].
Работа поворота
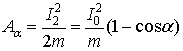 ,
,
![]() (3)
(3)
Таблица 1
|
α |
0° |
30° |
45° |
60° |
90° |
180° |
270° |
360° |
|
|
0 |
|
|
K0 |
2K0 |
4K0 |
6K0 |
8K0 |
В учебниках физики для силы F
, направленной под некоторым углом α
к перемещению S, формулу для работы перемещения записывают в виде: ![]() . В связи с этим утверждают, что центростремительные
силы, вызывающие движение тела по окружности (например, сила Лоренца при
вращательном движении заряда в магнитном поле, или сила тяготения при движении
спутника вокруг Земли по круговой орбите) работы не совершают, т.к. они всегда
перпендикулярны вектору скорости, а
. В связи с этим утверждают, что центростремительные
силы, вызывающие движение тела по окружности (например, сила Лоренца при
вращательном движении заряда в магнитном поле, или сила тяготения при движении
спутника вокруг Земли по круговой орбите) работы не совершают, т.к. они всегда
перпендикулярны вектору скорости, а ![]() .
.
Движение спутника - это бесконечное падение тела под действием силы
тяжести. Движение спутника аналогично движению тела, брошенного с башни высотой
h в
горизонтальном направлении с начальной скоростью
V0. При падении тела на Землю сила тяжести совершает
работу
![]() . Непонятно, почему сила тяжести не совершает работу
при движении спутника. Эти процессы аналогичны.
. Непонятно, почему сила тяжести не совершает работу
при движении спутника. Эти процессы аналогичны.
В работе [3] вывод формулы для вычисления работы
центростремительной силы
F тремя методами.
В итоге получается формула (3). Так как
![]() , то (3) можно переписать в виде
, то (3) можно переписать в виде
![]() . При
. При
![]() получаем
получаем
![]() - обычная
формула для работы, где S
- вертикальное
перемещение, равное радиусу орбиты. При одном обороте
- обычная
формула для работы, где S
- вертикальное
перемещение, равное радиусу орбиты. При одном обороте ![]() и работа будет
равна
и работа будет
равна
![]() .
.



