Scientific journal

Modern high technologies

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

Введение

Эффективность параллельного алгоритма зависит от многих параметров. Одним из таких параметров является равномерная загрузка процессоров вычислительной системы. При этом важно с одной стороны сохранив высоту параллельного алгоритма минимизировать его ширину. Другим важным параметром является время выполнения процессов. Если предполагать, что время выполнения всех процессов, отраженных в информационном графе в виде отдельных вершин, одинаково, тогда ориентированный ациклический информационный граф является наиболее подходящим инструментом для построения оптимального по высоте и ширине параллельного алгоритма. Но на практике такие условия - крайняя редкость. Следовательно, из-за неравномерности выполнения отдельных процессов, часть процессоров будет простаивать в ожидании результатов от своих предшественников. Поэтому, сама собой напрашивается замена ориентированного ациклического информационного графа его взвешенным аналогом, в котором в качестве весов будет выступать время выполнения процессов.

Временные диаграммы

Рассмотрим взвешенный информационный граф некоторого вычислительного процесса (рис.1).

При анализе вычислительного процесса, соответствующего данному информационному графу возникают следующие вопросы:

ü Насколько непрерывно работают три процессора, задействованные в вычислительном процессе системе? Сколько времени простаивает каждый процессор в процессе работы алгоритма?

Рис. 1. Взвешенный орграф

ü Можно ли сократить общее время работы алгоритмы путем уменьшения времени простоев процессоров?

ü Можно ли сократить ширину алгоритма путем уменьшения времени простоев процессоров за счет объединения мелких (по времени работы) операций в более крупные?

Для ответа на эти вопросы построим сначала временную диаграмму (рис.2), где t - время выполнения каждого процесса, n - номер процессора, задействованного в вычислении.

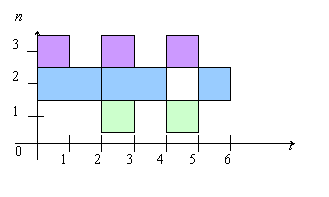
Рис. 2. Временная диаграмма работы процессоров.

Построенная временная диаграмма показывает:

ü Суммарное время работы алгоритма равно 6 ед.

ü Первый процессор простаивает дважды и суммарное время простаивания составляет
3 ед., второй процессор простаивает единожды
1 ед., третий - дважды и суммарное время простаивания равно 2 ед.

Таким образом, оптимизация процесса только по числу процессоров не является конечным результатом улучшения качества параллельного алгоритма.

Из рис. 2 видно, что два процесса, вычисляемы на одном процессоре (А и В) можно объединить в один, тем самым, произведя укрупнение схемы вычислений (рис.3). 

Рис. 3. Взвешенный орграф

Временная диаграмма при этом примет вид (рис.4):

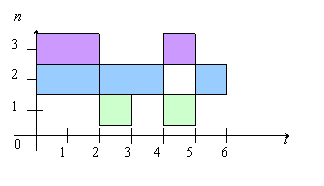
Рис. 4. Временная диаграмма работы процессов

Вследствие этого укрупнения, на первом ярусе два процессора работают одинаково. Алгоритм оптимизации полученного информационного графа (рис.3) с помощью матричного алгоритма по числу процессов позволяет преобразовать его к следующему виду (рис.5):

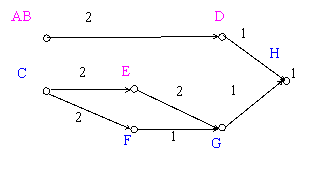
Рис. 5. Взвешенный орграф

Ширина алгоритма при этом становится равной 2. Следовательно, в вычислениях могут быть задействованы два процессора, что увеличит плотность вычисления и сделает применение вычислительной техники более эффективным. Временная диаграмма работы процессоров примет вид (рис.6).

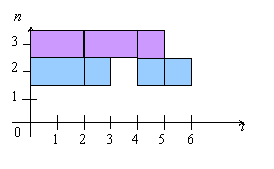
Рис. 6. Временная диаграмма работы процессоров

Вследствие этого, можно ответить на третий из поставленных вопросов: ширину информационного графа возможно сократить.

Автоматизировать процесс оптимизации информационного графа по высоте с помощью временных диаграмм достаточно сложно. Формализовать этот процесс можно, если заменить информационный граф на граф работы процессоров (рис.7). 

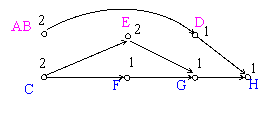
Рис. 7. Граф работы процессоров

При этом остается открытым вопрос об эффективности используемой памяти вычислительной системы. И скорее всего, схема использования памяти в данном случае будет хуже, чем в первоначальном варианте (рис.1).

Алгоритм оптимизации высоты
информационного графа

Матрица смежности, соответствующая информационному графу с рис.1 имеет вид:

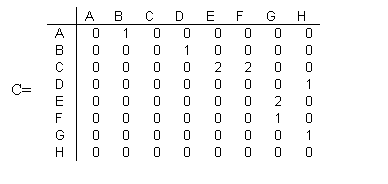
Т.к. каждая вершина графа соответствует одному процессу, выполняемому за определенное время, то в любой отдельно взятой строке все ненулевые элементы равны между собой. Это свойство взвешенного по времени информационного графа.

Алгоритм оптимизации высоты графа, является продолжением матричного алгоритма оптимизации ширины графа и заключается в следующем:

1)       Разбить вершины графа на группы с помощью алгоритма оптимизации ширины информационного графа.

2)       Начиная с первого яруса, найти группу вершин с разными временными значениями. Отметить ее.

3)       В найденной группе найти максимальное значение по времени.

4)       Отметить вершину, временное значение которой меньше максимального и рассмотреть возможность ее объединения с вершиной из следующей группы по принципу:

Если в строке матрицы смежности, соответствующей отмеченной вершине есть ненулевой элемент, соответствующий вершине из следующей группы и в столбце, соответствующем этой вершине, отсутствуют ненулевые элементы в строках отмеченной группы, то отмеченную вершину можно объединить с проанализированной вершиной из следующей группы.

Формально, это условие выглядит так:

Пусть - отмеченная вершина группы G₁, - вершина из следующей группы G₂, - элементы матрицы смежности, стоящие на пересечении строк вершин группы G₁ и j-го столбца, тогда:

5)       Повторить четвертый шаг для всех вершин отмеченной группы.

6)       Повторить шаги 3-5 для всех следующих групп, кроме последней.

7)       Повторять алгоритм до тех пор пока не останется ни одного объединения.

Пример. Рассмотрим процесс работы алгоритма на информационном графе с рис. 1.

1)       Разобьем вершины графа на группы с помощью матричного алгоритма оптимизации ширины информационного графа. В результате можно выделить следующие группы: AC, BEF, DG, H.

Ширина графа равна трем, высота - четырем, общее число вершин - восемь. Следовательно, оптимальная ширина при данной высоте равна двум (8/4=2). Данная ширина не может быть достигнута, т.к. выходная вершина всего одна, и, следовательно, на оставшиеся три яруса будет приходиться семь вершин и реальная высота: trunc(7/3)=trunc(2.3)=3. Поэтому, вторую часть матричного алгоритма оптимизации ширины графа можно не применять, т.к. реальная и оптимальная ширина.

2)       Возьмем первую группу. Время выполнения операций A и C разное: 1 и 2.

3)       В отмеченной группе найдем максимальное значение по времени: t_c=2.

4)       Отметим вершину, временное значение которой меньше максимального : А. Рассмотрим возможность ее объединения с вершиной из следующей группы. В следующей группе четыре вершины. В строке, соответствующей вершине А существует только одна единица - в столбце вершины В. В этом столбце других ненулевых элементов нет. Следовательно, вершину В можно переместить в отмеченную группу и объединить с вершиной А.

5)       Больше подобных вершин нет. Алгоритм закончен.

Процесс выполнения шагов 2-5 отображен в таблице. 

Алгоритм оптимизации высоты информационного графа

В результате выполнения данного алгоритма получен граф с рис.7.

Ширина графа стала равной 2, что увеличивает эффективность работы вычислительной системы.

Заключение

Апробация полученных алгоритмов показала, что применение алгоритма оптимизации информационного графа по ширине, как правило, сокращая ширину графа, оставляет достаточно много простоев процессоров. Добиться наилучшего результата можно, только проведя после первого шага оптимизацию по времени или применив комбинированный метод. В зависимости от структуры информационного графа в разных случаях превалируют или тот или другой метод. В результате применения алгоритма оптимизации информационного графа по времени выполнения в ряде случаев могут сокращаться как высота алгоритма, так и ширина.

СПИСОК ЛИТЕРАТУРЫ

1. Лупин С.А., Посыпкин М.А. Технологии параллельного программирования. - М.: ИД «Форум»: ИНФРА-М, 2008. - 208 с.

2. Касьянов В.Н., Евстигнеев В.А. Графы в программировании: обработка, визуализация и применение. - СПб.: БХВ-Петербург, 2003. - 1104 с.

3. Эндрюс Г.Р. Основы многопоточного, параллельного и распределенного программирования.: пер.с англ. - М.:Издательский дом «Вильямс», 2003. - 512 с.