Систолическая матрица для ЦОС модулярной арифметике ПСКВ использует механизм обнаружения и коррекции ошибок на фоне вычислений. Вычисления ведутся по 7 взаимно простым основаниям с рабочими модулями 
и контрольными 
, где 
, 
, 
, 
, 
, при этом обеспечивается динамический диапазон 21 бит. В качестве контрольных выбраны два модуля 
, 
.
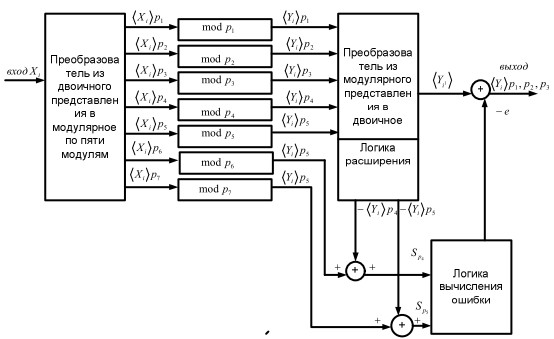
Рис. 1. Фильтр на основе систолической матрицы с цепями обнаружения и коррекции ошибок
Систолические принципы организации вычислений в модулярной арифметике с взаимно простыми основаниями позволяют разбить всю задачу на элементарные простые подзадачи, которые могут выполняться на одинаковых процессорах простой структуры, каждый из которых связан только с ближайшими соседями, что упрощает разработку внешних связей и контроля, снижает задержки сигналов и облегчает проблемы, связанные с перекосом синхроимпульсов.
На входе систолической матрицы с цепями обнаружения и коррекции ошибок на фоне вычислений включен преобразователь, конвертирующий двоичное представление в пять последовательностей остатков и выходной интерфейс для преобразования пяти обработанных помодульных последовательностей в двоичное представление. Систолические принципы организации вычислительного процесса предполагают множество вариантов обработки. В данном варианте выбрана модель, в которой частичные результаты остаются в ячейках матрицы, а данные и веса «прокачиваются» через матрицу в различных направлениях, причем веса сдвигаются быстрее.
Каждая ячейка систолической матрицы является независимым процессорным элементом. Столбец из пяти ячеек ( по количеству модулей системы ) составляет процессорный блок, выходы которого выдают обработанную информацию в выходной конвертор. После полного окончания вычислений каждая ячейка выдает результаты в один из нескольких выходных регистров, через которые выходные данные поступают непосредственно в выходной преобразователь систем счисления. Выходной конвертор получает пять немодифицированных остатков одновременно и преобразует их в соответствующие двоичные эквиваленты.
Коррекция ошибок вычислений происходит следующим образом. Ошибки могут происходить в любой индивидуальной ячейке или при передаче данных между ячейками. Большинство ошибок, могущих возникнуть внутри ячейки, влияют только на выход одного из каналов. Данная реализация процессора устойчива к ошибкам и решает много проблем, связанных с получением безошибочного результата в процессорных ячейках. Путь данных в процессоре не адресуется, что исключает появление ошибок в других каналах при ошибке в одном.
Свойства модулярного представления таковы, что два канала в вычислительной модели могут быть выполнены избыточными, что будет означать тройную эффективную избыточность. Достаточным условием для двух избыточных модулей является то, что они взаимно просты между собой и между неизбыточными модулями и больше, чем неизбыточные модули. Со способностью корректировать некоторые одиночные ошибки в остатках система становится устойчивой к некоторым видам ошибок ячеек, например, при одной неисправной ячейке в блоке корректирующие модели могут включать ячейки из некоторой комбинации каналов.
Способность данной систолической матрицы корректировать ошибки выгодно отличает ее от других видов систолических матриц, которые работают по принципу передачи частных результатов в другие ячейки и в которых коррекция ошибок затруднена.
Для обеспечения возможности корректировать ошибки приходится вводить два избыточных канала. Избыточными являются каналы по модулям 
. По ним формируются синдромы ошибок, которые показывают значение ошибки и номер ошибочного канала. Выходная логическая схема вычитает значение синдрома из значения ошибочного канала. В итоге выходная информация всегда истинна, даже при выходе из строя нескольких вычислительных ячеек в разных каналах. На этой архитектуре был реализован цифровой фильтр с конечной импульсной характеристикой. Такой принцип коррекции ошибок желателен для всех систем модулярной арифметики.
СПИСОК ЛИТЕРАТУРЫ:
- Элементы компьютерной математики и нейроноинфроматики /Червяков Н.И., Калмыков И.А., Галкина В.А., Щелкунова Ю.О., Шилов А.А.; Под ред. Н.И. Червякова. - М.: Физматлит, 2003. - 216 с.
- Калмыков И.А. Математические модели нейросетевых отказоустойчивых вычислительных средств, функционирующих в полиномиальной системе классов вычетов/Под ред. Н.И. Червякова - М: Физматлит, 2005.-276 с.