Для анализа нестационарных процессов, в которых информативным является сам факт изменения частотно-временных характеристик сигнала (примерами таких сигналов являются речь, музыка, изображение), требуются базисные функции, способные выявлять как частотные, так и временные характеристики, т.е. обладающие частотно-временной локализацией. Одним из способов решения данной задачи является использование математического аппарата вейвлет-функций, в частности, вейвлет-разложения сигнала, при котором, в отличие от оконного преобразования Фурье, базисную функцию не только смещают во времени, но и масштабируют, чтобы получить многократное перекрытие сигнала. Вид вейвлет-преобразования на плоскости «время-частота» приведён на рис. 1.
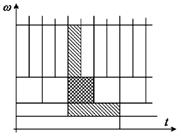
Рис. 1. Представление вейвлет-преобразования на плоскости «время-частота»
Непрерывным вейвлет-преобразованием (CWT, continuous wavelet transform) функции 
называют функцию двух переменных:
, 
где вейвлеты 
являются масштабированными и сдвинутыми копиями порождающего (материнского) вейвлета 
:
, .
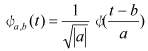Если для порождающего вейвлета выполняется условие
,
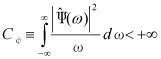где 
- образ Фурье вейвлета ψ(t), то вейвлет-преобразование обратимо, т.е. существует обратное непрерывное вейвлет-преобразование:
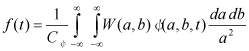
Таким образом, непрерывное вейвлет-преобразование - это разложение сигнала по всем возможным сдвигам и сжатиям (растяжениям) некоторой функции. Количество копий порождающего вейвлета, необходимое для обратимого разложения, можно существенно сократить.
Распространённый случай - вычисление значений W(a,b) только для a и b вида:
, 
, 
Вместо непрерывной функции получается конечное множество значений:
(1)
где
, 
Обратное преобразование примет вид:
(2)
Формулы (1) и (2) определяют диадное (или дискретное) ортогональное вейвлет-преобразование.
Вейвлет-преобразование сигналов может быть представлено как банк фильтров. Простой одноуровневый банк фильтров показан на рис. 2.
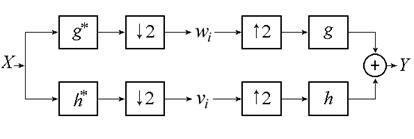
Рис. 2. Представление вейвлет-преобразования в виде банка фильтров
На рис. 2 показано, каким образом вейвлет-преобразование использует два фильтра: низкочастотный фильтр h* и высокочастотный фильтр g*, за которыми следует децимация сигнала (subsampling). В левой части схемы сигнал подвергают фильтрации, а затем децимации, т.е. отбрасывают часть отсчётов отфильтрованного сигнала, оставляя, например, только чётные отсчёты. Очевидно, что подобная схема неэффективна, и предпочтительнее производить децимацию перед фильтрацией (рис. 3).
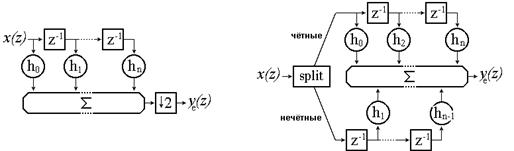
Рис. 3. Стандартный КИХ-фильтр с децимированным сигналом на выходе (слева) и его более эффективная реализация (справа)
Если применить полученную новую модель КИХ-фильтра к вейвлет-преобразованию в виде банка фильтров (рис. 3), то данное преобразование можно записать в следующей векторной форме:
,
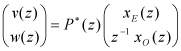где P*(z) - полифазная матрица:
.
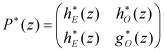Важным свойством определённых выше преобразований является то, что отсчёты записывают в единый поток данных, замещая предыдущие значения. Все отсчёты этого потока заменяются новыми отсчётами, и в любой момент времени необходимы только текущие отсчёты для осуществления дальнейших вычислений. Это свойство сходно со свойством быстрого преобразования Фурье, где преобразованные данные также замещают исходные. Таким образом, происходит существенная экономия памяти при осуществлении преобразований, что является важнейшим фактором при построении лифтинговых вейвлет-преобразований на устройствах с ограниченными вычислительными ресурсами (например, на мобильных телефонах или карманных компьютерах).
СПИСОК ЛИТЕРАТУРЫ:
- Родионов И.В. Проблемы эффективной передачи малоформатного видео в сетях сотовой связи 3-го поколения. // Proceedings 2005 of St.Petersburg IEEE Chapters ´110 Anniversary of Radio Invention´ Volume 3, IEEE Russia Northwest 2005. http://www.procongress.info/events/radio_pr/files/rodionov.doc
- Бабин А.И. Передача малоформатного потокового видео в сетях мобильной связи 3G стандарта IMT-2000/UMTS .// Тезисы 21-й международной конференции РАЕН, Эль-Гуна, 2007.