Процесс "подгонки" параметров (или задача параметрической идентификации пластовой системы) осложняется тем, что система - пласт - недоступна для прямых замеров, а косвенные замеры осуществляются лишь в некоторых точках пласта - скважинах. К косвенным замерам традиционно относят обводненность продукции, статические и динамические уровни. К определяемым параметрам - пористость, проницаемость, некоторые свойства пластовых жидкостей. Все косвенные замеры имеют существенную степень погрешности [2]. Анализ чувствительности моделей к таким погрешностям осуществляется редко в силу значительного объема вычислений даже для решения обычной задачи имитации пластовой системы. Однако следует помнить о том, что задача идентификации - некорректная задача и дополнительное исследование необходимо в любом случае. Здесь мы постараемся дать некоторые методы анализа пластовых моделей к погрешностям в исходных данных, требующие ограниченного объема вычислений.
Рассмотрим двумерную двухфазную пластовую систему при отсутствии капиллярных сил:
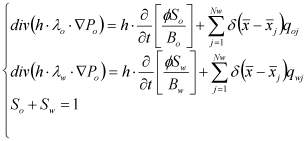
Здесь: 
-давление в фазе ph; 
- насыщенность фазой ph; f=f(po)-пористость, в общем случае зависящая от давления; qphj=qphj(t) - дебит фазы, зависящий от времени; Bph=Bph(pph) - объемный коэффициент фазы ph; 
- подвижность фазы ph; krph=krph(Sw) - относительная фазовая проницаемость; mph=mph(pph) - вязкость фазы; 
- проницаемость, 
- мощность пласта.
Отметим здесь, что задача имитации состоит в нахождении функций 
и 
по остальным известным функциям. Инверсная задача параметрической идентификации состоит в нахождении каких-либо функций из множества 
по некоторым функционалам от решений 
.
В рассматриваемой ситуации в качестве уточняемых (идентифицируемых) параметров модели выступают пористость и проницаемость каждой ячейки пластовой системы, функциями, исследуемыми на чувствительность, являются давление и насыщенность. Обычно на месторождении замеряются дебиты жидкости, обводненность продукции и забойные (устьевые) давления. Поэтому представляется целесообразным оценивать чувствительность именно этих замеряемых величин. связь соответствующих величин устанавливается посредством следующих соотношений - для чувствительности забойного давления:
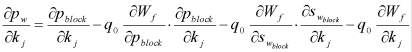
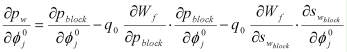
Чувствительность обводненности:
,
,
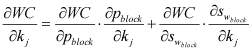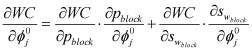при этом: pw - забойное давление, WCT - обводненность, pblock - давление в ячейке, проперфорированной скважиной, Wf - приведенный радиус, нижний индекс j указывает на соответствующую ячейку. Важно подчеркнуть, что указанные формулы позволяют рассчитывать чувствительность не только к параметру в одной ячейке j, но и к параметру в произвольной области залежи при соответствующем уровне параметризации.
Для применения указанных формул необходимо рассчитать величины 
, 
, 
, 
.
Одним из возможных вариантов может служить их замена конечной разностью, например:
.
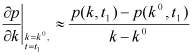В этом случае для нахождения производной требуется решить две задачи имитации и определить p(k) и p(k0). При большом числе параметров это может стать весьма трудоемким вычислительным процессом. Поэтому вызывает интерес нахождение альтернативных способов вычисления коэффициентов чувствительности.
В качестве одного из них предлагается следующий. Строится итерационный процесс с использованием соотношения:
,
где
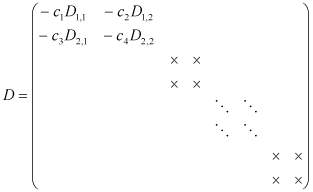
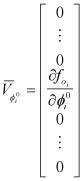
При этом 
, J является матрицей Ньютона, рассчитываемой при решении обычной задачи имитации (методом FIM или IMPES) [3], f - уравнение материального баланса для соответствующей ячейки.
Для случая FIM функции 
и 
в ячейке i имеют вид:
;
,
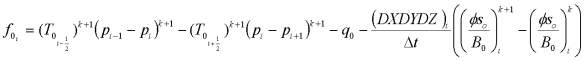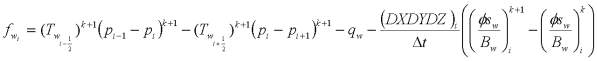где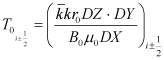 
; 
;
; 
; 
;
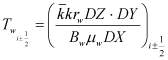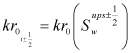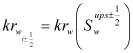- водонасыщенность в ячейке с большим давлением;
q0(w) - сток или источник (если он есть в ячейке i).
Для случая IMPES функции 
и 
имеют вид:
.
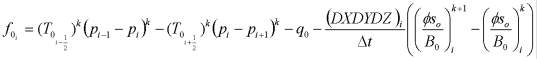
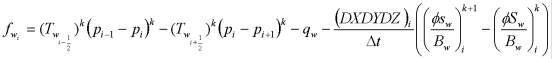матрица D трехдиагональна, в частности, для случая FIM:
; 
; 
; 
.
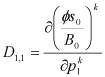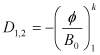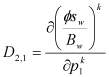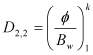Для IMPES:
; 
; 
;
,
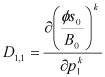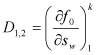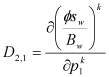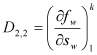сi - некоторые константы; верхний индекс k - индекс итерации.
Предлагаемый способ имеет следующие особенности:
- Для нахождения КЧ требуется решение лишь одной задачи имитации;
- матрицы J и D остаются постоянными на каждый временной шаг (k) и рассчитываются во время решения задачи имитации;
- кроме
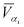, все остальные члены итерационного соотношения считаются во время решения задачи имитации.
Таким образом, на основе специального анализа матрицы G предложен способ расчета коэффициентов чувствительности, не требующий значительных вычислительных затрат (как в случае конечных разностей). При наличии численной модели предложенный алгоритм достаточно просто реализуется. Полученные таким образом коэффицинты чувствительности могут использоваться (с привлечением дополнительных программных процедур) для автоматической адаптации, либо для подходящей (с точки зрения адаптации) параметризации модели и выявления наиболее чувствительных параметров.
СПИСОК ЛИТЕРАТУРЫ:
- Мангазеев В.П., Кошовкин И.Н. Внедрение компьютерных технологий для решения задач геологии и разработки месторождений // Нефтяное хозяйство. - 1996, № 11. - С.64-66.
- Aziz K., Settari A. Petroleum Reservoir Simulation. - New York: Elsevier Applied Science Publishers, 1979. - 362p.
- ECLIPSE 100 Technical Description. - London: Schlumberger GeoQuest, 2002. - 978p.