При компьютерном моделировании применена двухконтурная структура управления (рис.1), контуры которой относятся к температуре и влажности соответственно. Регулирование осуществляется с использованием цифровых регуляторов, реализующих нелинейный пропорционально-интегральный закон управления.
Введение нелинейности
В непрерывном времени нелинейный динамический закон управления описывается формулой:
![]() ,
,
где u(t) - управляющее воздействие,
ε (t) - рассогласование между заданием и выходом объекта,
kp - коэффициент усиления пропорциональной части,
ki - коэффициент при интегральной части,
![]() - коэффициенты при нелинейной части.
- коэффициенты при нелинейной части.
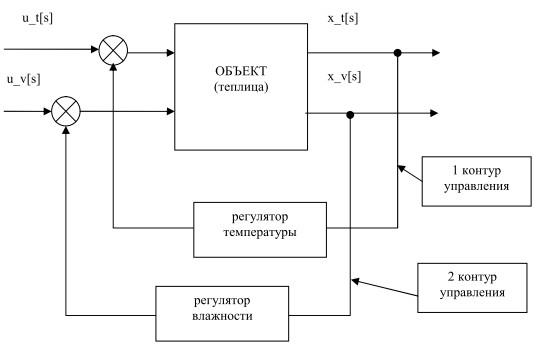
Рис.1. Структура двухконтурного управления.
Нелинейный динамический закон получен из линейного ПИ-закона управления путем введения зависимости эффективных коэффициентов усиления от рассогласования между задающим воздействием и выходом объекта на предыдущем такте и на текущем такте.
Проиллюстрируем на примере корректирующей добавки к цифровому ПИ-закону управления. В цикле по тактам дискретного времени s=0,1,...,N -1 дискретой отсчета Dt.Цифровая форма нелинейного динамического алгоритма управления для 1 контура (управление по температуре) имеет вид:
u_t[s+1] = u_t[s] + (k_tp + k_ti*Dtx + k_tnl_1*|e_t[s+1] |)*ε_t[s+1] -
- (k_tp + k_tnl_2*|e_t[s] |)*ε_t[s] + ∆u_t[s].
Цифровая форма нелинейного динамического алгоритма управления для 2 контура (управление по влажности) имеет вид:
u_v[s+1] = u_v[s] + (k_vp + k_vi*Dtx + k_vnl_1*|ε_v[s+1]|)*ε_v[s+1] -
- (k_vp +k_vnl_2*|ε_v[s]|)*e_v[s] + ∆u_v[s].
где u_t[s],u_v[s] - управляющее воздействие для 1 и 2 контура соответственно,
![]() - рассогласование между заданием и выходом объекта по 1 контуру (по температуре),
- рассогласование между заданием и выходом объекта по 1 контуру (по температуре),
![]() - рассогласование между заданием и выходом объекта по 2 контуру (по влажности),
- рассогласование между заданием и выходом объекта по 2 контуру (по влажности),
k_tp , k_vp - коэффициенты усиления при пропорциональной части,
k_ti , k_vi - коэффициенты при интегральной части,
k_tnl_1 , k_tnl_2, k_vnl_1 ,k_vnl_2- коэффициенты при нелинейной части.
xz_t[s], xz_v[s] - задающее воздействие,
x_t[s], x_v[s] - выход объекта.
Отметим, что в цифровых системах управления необходимо учитывать ограниченность и квантованность управляющих воздействий по уровню сигнала, тогда:
![]()
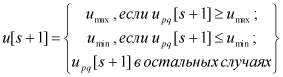
![]()
Здесь {umin, umax} - границы изменения управляющего воздействия, Δuq - шаг квантования управляющего воздействия по уровню сигнала. Данные параметры добавляются к стандартным параметрам ПИ-закона управления.
Основным отличием от универсального цифрового ПИ-закона управления является введение нелинейности, реализованной за счет использования нелинейного коэффициента. Роль данного коэффициента состоит в форсировании управляющих воздействий при больших отклонениях выхода управляемого параметра от задания и в смягчении управляющих воздействий по мере уменьшения данного рассогласования.
При моделировании необходимо учесть наличие противоречия между использованными показателями качества. Настройка системы осуществляется на оптимальное значение одного из показателей, при этом фиксируется потеря качества по другим показателям. Далее с использованием, например, метода уступок определяется значение параметров, удовлетворяющие требованиям технологического процесса. Показатели качества, использованные в работе время переходного процесса, среднее абсолютное значение отклонения выхода объекта от задания, среднее квадратическое отклонение выхода объекта от задания.
Проводятся сравнительный анализ с универсальным цифровым ПИ-регулятором, позволяющий обосновать введение нелинейности.
Исследование работы системы управления микроклиматом теплицы осуществляется на основании математической модели объекта, реализованной в пакете математических и инженерных расчетов MathCad.
Математическая модель учитывает особенности системы управления микроклиматом теплицы необходимого для обеспечения оптимального технологического процесса выращивания овощных культур.
Результаты моделирования будут использованы при реализации масштабной модели системы управления микроклиматом теплицы.



