, (1)
где Lz -главный момент количества движения системы винт - зерно;
- сумма моментов внешних сил.
Кинетический момент вращающейся спирали равен:
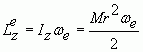, (2)
где Iz - момент инерции спирального винта; М - масса спирального винта; ωe - угловая скорость винта.
С учетом значения скоростей исходное уравнение (1),принимает вид:
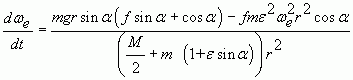(3)
Это и есть дифференциальное уравнение движения зерна по винтовой линии. Если считать вращательное движение винтового валика равномерным, т. е. ωe = const, то 
. Следовательно,
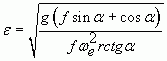. (4)
С учетом уравнения (4) угловая скорость зерна при относительном движении принимает вид:
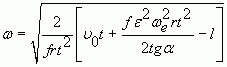(5)
Из выражения (4) видно, что соотношение угловых скоростей относительного и переносного движения обратно пропорционально частоте вращения.
Следовательно, с увеличением угловой скорости спирального винта зерно ускоряет свое движение и как бы догоняет винтовую линию.
Полученные зависимости могут быть использованы при проектировании и изготовлении спирального транспортера.