При построении фрактальной модели микроускорений с помощью функции Вейерштрасса-Мандельброта важно адекватно отождествить параметры функции с реальными физическими характеристиками возникновения поля микроускорений внутри космического аппарата (КА) при его орбитальном полете [1]. В ряде работ, посвященных этому отождествлению, фрактальная размерность функции D связывается с моментом от управляющих ракетных двигателей системы ориентации и управления движением КА (УРД) [2-4]. Рассматривается поле микроускорений создаваемое за счет колебаний больших упругих элементов (панелей солнечных батарей (ПСБ), радиатора, антенн и др.) сразу после выключения УРД [1].
Постановка задачи
Для исследования влияния погонной массы упругого элемента на среднее значение модуля микроускорений, создаваемых внутри КА при колебаниях этого элементы, была выбрана схема КА типа «НИКА-Т» с одним упругим элементом. Вектор момента от УРД был параллелен линии крепления упругого элемента к корпусу КА. Уравнения движения такого КА получены в работе [5]. Здесь упругий элемент рассматривается как жестко заделанная в корпус КА пластина.
Исследования, проведенные в [6] показали, что учет упругости узла крепления ПСБ не дает существенных поправок в модель создания поля микроускорений, немного снижая амплитуду микроускорений и частоту передаваемых на корпус колебаний. Неучет данного снижения делает оценку более надежной, закладывая определенный запас.
Таким образом, ставиться задача исследования изменения среднего значения модуля микроускорений, возникающих из-за колебаний упругого элемента, при изменении погонной массы этого элемента.
Основные результаты работы
На рис. 1 показаны зависимости среднего значения микроускорений от момента УРД при различных значениях погонной массы упругого элемента. Как видно, такой ход событий полностью соответствует изменению среднего значения ФВМ в зависимости от фрактальной размерности D, которая приведена на рис. 1 работы [7]. Тогда роль масштабного параметра b здесь играет как раз погонная масса упругого элемента.
Аналогичные зависимости получены и при другой длине упругого элемента (рис. 2-5).
Эти зависимости практически прямолинейны. Сам модуль микроускорений при вращательном движении КА вокруг центра масс складывается из нормальной и касательной компонент. Как известно, нормальное ускорение зависит от квадрата угловой скорости вращения КА и в данной задаче является малой величиной более высокого порядка малости по сравнению с касательным ускорением. В свою очередь касательное ускорение линейно связано с угловым ускорением вращения КА, которое также линейно зависит от момента УРД в данной постановке задачи, где считается, что все другие моменты малы по сравнению с моментом УРД.
Несмотря на то, что при получении зависимостей, представленных на рис. 1-5, учитывались обе компоненты, влияния нормальной компоненты совершенно незаметно. В дальнейшем эти корреляционные зависимости можно считать идеальными прямыми, начинающимися в точке ( 0; 0 ).
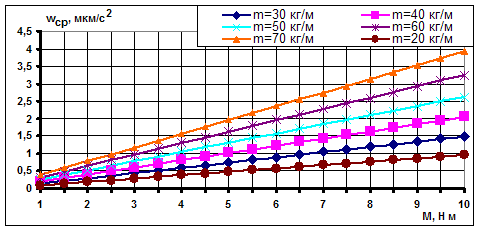
Рис. 1. Динамика изменения среднего значения микроускорений от момента УРД при общей массе КА 6500 кг и длине ПСБ 4,6 м
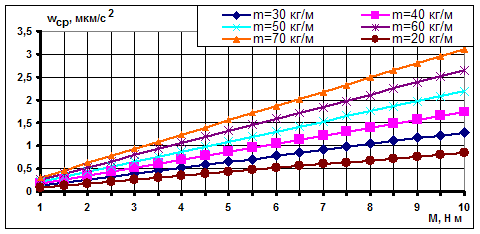
Рис. 2. Динамика изменения среднего значения микроускорений от момента УРД при общей массе КА 6500 кг и длине ПСБ 3,6 м
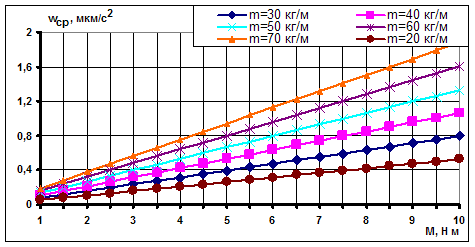
Рис. 3. Динамика изменения среднего значения микроускорений от момента УРД при общей массе КА 6500 кг и длине ПСБ 2,6 м
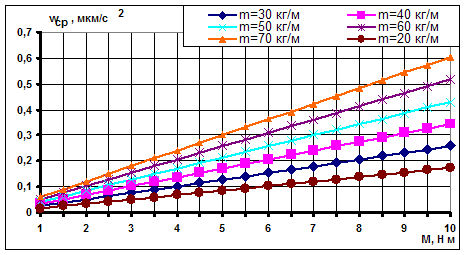
Рис. 4. Динамика изменения среднего значения микроускорений от момента УРД при общей массе КА 6500 кг и длине ПСБ 1,6 м
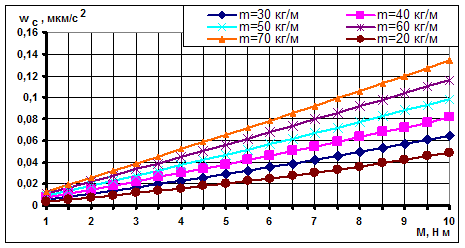
Рис. 5. Динамика изменения среднего значения микроускорений от момента УРД при общей массе КА 6500 кг и длине ПСБ 0,6 м
С помощью метода наименьших квадратов были определены коэффициенты линейной модели парной регрессии:
![]() , (1)
, (1)
где М - момент УРД.
На рис. 6 представлена зависимость коэффициента a1 от погонной массы упругого элемента при различной длине этого элемента.
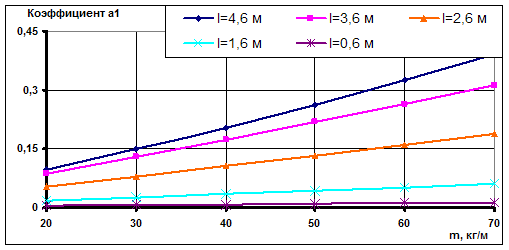
Рис. 6. Динамика изменения коэффициента а1 при варьировании параметрами упругого элемента
Одним из показателей качества аппроксимации зависимостей рис. 1-5 функциональной зависимостью (1) является величина другого коэффициента a0. При идеальной аппроксимации значение этого коэффициента должно быть равно нулю, т.к. выше было указано на то, что все корреляционные прямые проходят через точку (0; 0).
На рис. 7 представлена зависимость коэффициента a0 от погонной массы упругого элемента при различной длине этого элемента.
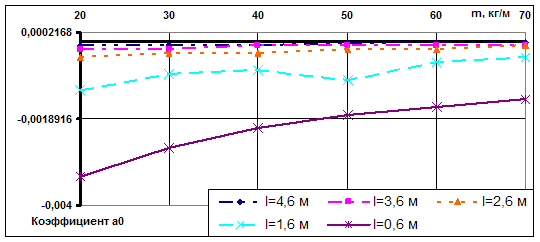
Рис. 7. Динамика изменения коэффициента а0 при варьировании параметрами упругого элемента
Основные выводы по работе
Проведенные исследования показывают, что зависимость между средним уровнем микроускорений, возникающих во внутренней среде КА из-за колебаний упругих элементов, и погонной массой упругих элементов представляет собой практически идеальные прямые линии (1). Оценка точности линейной модели с помощью коэффициента a0 (рис. 7) позволяет сделать вывод о том, что неточности аппроксимации, скорее всего, связаны с округлением при построении корреляционных зависимостей рис. 1-5, чем с влиянием нормальной компоненты микроускорений.
С другой стороны, необходимо отметить, что влияние погонной массы упругого элемента на зависимость среднего значения микроускорений от момента УРД аналогично влиянию масштабного параметра b ФВМ на зависимость ее среднего значения от фрактальной размерности D [7]. Поэтому можно говорить о качественном отождествлении двух этих параметров при построении фрактальной модели микроускорений с помощью ФВМ.
Следует, однако, заметить, что, в отличие от связи момента УРД с фрактальной размерностью ФВМ D, масштабному параметру b соответствует не только погонная масса упругого элемента. По-видимому, он связан с любым параметром КА, характеризующим массовую долю упругого элемента в общей массе самого КА.
Дальнейшим этапом работы является исследование влияния длины упругого элемента, а также изменения общей массы КА при неизменных параметрах упругого элемента на модуль микроускорений. Эти исследования позволят сформировать единый, физически реальный параметр, соответствующий масштабному коэффициенту b ФВМ.
СПИСОК ЛИТЕРАТУРЫ:
- Седельников А.В. Фрактальная оценка микроускорений для слабого демпфирования собственных колебаний упругих элементов космического аппарата I // Изв. вузов Авиационная техника. - 2006. - N 3. - с. 73-75.
- Седельников А.В. Качественное отождествление параметров функции Вейерштрасса-Мандельброта при оценке микроускорений // Научные чтения в Самарском филиале РАО. - Часть 1. Естествознание. - М.: Изд. УРАО. - 2006. - 137 - 158.
- Седельников А.В., Подлеснова Д.П. Выявление физического смысла параметров функции Вейерштрасса-Мандельброта при оценке с помощью нее микроускорений // Материалы XXXI-х Академических чтений по космонавтике. - Москва. - 2007. - с. 88-89.
- Седельников А.В., Подлеснова Д.П. Основные принципы построения аналитической зависимости параметров функции Вейерштрасса-Мандельброта для оценки микроускорений // Успехи современного естествознания. - № 12. - 2006. - с. 82 - 83.
- Авраменко А.А., Седельников А.В. Моделирование поля остаточной микрогравитации на борту орбитального КА // Изв. Вузов Авиационная техника. - 1996. - №4. - с. 22-25.
- Седельников А.В., Ефимова Е.А. Учет влияния упругости узла крепления упругих элементов космического аппарата на оценку микроускорений внутри рабочей зоны технологического оборудования при моделировании условий для технологических процессов // Сборник статей III-й Всероссийской научно-практической конференции «Инновации в машиностроении». - Пенза. - 2003. - с.115-117.
- Седельников А.В., Поделеснова Д.П., Ярош Н.С. Исследование зависимости коэффициентов линейной модели парной регрессии от параметров функции Вейерштрасса-Мандельброта при моделировании среднего значения функции с помощью ее фрактальной размерности // Успехи современного естествознания. - № 9. - 2006. - с. 100-103.



