В [1,2] показано, что ряд физико-химических систем, которые могут быть описаны уравнениями в дробных производных, должны содержать в себе каналы, входящие в состав ветвящейся фрактальной структуры.
Такими системами могут быть процессы теплопереноса и массопереноса в перколяционных кластерах, фрактальных и пористых средах. Причем [1,2] получено, что показатель дробной производной по времени соответствует доли каналов (ветвей), открытых для протекания. В [5] показано, что аномальная диффузия (диффузия Леви) имеет фрактальную природу, и получена взаимосвязь порядка дробной производной с показателями масштабного преобразования времени и Херста.
Рассмотрим обобщенную задачу диффузии на полупрямой:
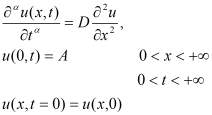(1)
где t- время, u(x,t)-концентрация диффундирующего компонента; 
- дробный порядок производной (характеризующий долю каналов, открытых для протекания), 0< <1, D2 -эффективный коэффициент диффузии на фрактале.
Для учета начального условия u(x,t =0) = u(x,0) необходимо его явно внести в уравнение и исходить из уравнения следующего вида:
Для нахождения решения этой задачи сначала применим синус преобразования по переменной x после применяя преобразования Лапласа получим:
После преобразования выражений 
, 
, получим:
= 
= 
,
= 
.
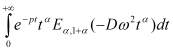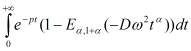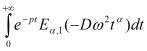Из этих равенств следует:
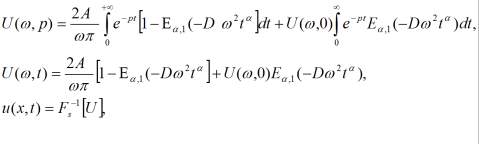
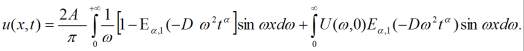(3)
где 
- функция Миттаг-Леффлера.
Рассмотрим случай, когда 
тогда
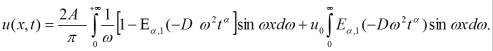
При 
получаем решение:
+ 
,
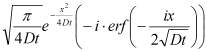где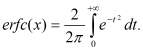 
А в остальных случаях, когда 0<α <1, мы получаем новый класс решений. Полученное решение (3) можно использовать при исследовании процессов диффузии в системах, обладающих фрактальной структурой.
СПИСОК ЛИТЕРАТУРЫ:
- Nigmatullin R.R. //Phys. Stat. Solidi (b). 1986. V. 133. P. 425.
- Nigmatullin R.R. // Ibid.1986. V.133. P.713.
- Бабенко Ю.И. Тепломассообмен. Методы расчета тепловых и диффузионных потоков. Л.: Химия, 1986. 144с.
- Нигматулин Р.Р. ТМФ. 1992. Т.90. №3. С.354.
- Суханов А.Д., Тимашев С.Ф. // Журнал физ. химии. 1998. Т.72. №11. С. 2073.
- Иванова В.С., Балакин А.С., Бунин И.Ж., Оксогоев А.А. Синергетика и фракталы в материаловедении. М.: Наука, 1994. 383 с.
- Самко С.Г., Килбас А.А., Маричев О.И. Интегралы и производные дробного порядка и некоторые их приложения. Минск: наука и техника, 1987.