Однако отсутствие стандартных пленочных образцов (и исключительная сложность изготовления градуировочных ненасыщенных слоев в лабораториях) резко ограничивает возможности использования существующих способов РСФА. В связи с этим повышается роль способов, основанных на теоретическом учете матричных эффектов, величина которых зависит от толщины исследуемой пленки.
Применительно к РСФА ненасыщенных (пленочных) образцов по аналогии с работой [1] обоснованы уравнения связи вида
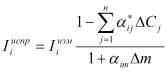, (1)
где 
- коэффициенты межэлементных влияний, характеризующие относительное изменение интенсивности флуоресценции элемента i при единичном изменении только самого содержания влияющего элемента j (т.е. коэффициенты, вычисленные в идеализированном предположении постоянства поверхностной плотности m образца);
- коэффициенты влияния поверхностной плотности образца.
В случае слабоизменяющегося элементного состава и поверхностной плотности образцов уравнения связи принимают вид
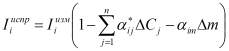. (2)
Эксперимент на математической модели в приближении возбуждения флуоресценции смешанным рентгеновским первичным излучением подтвердил корректность развиваемого подхода.
Элементами образцов служили 
. Коэффициенты межэлементных влияний находили путем численного дифференцирования с использованием модели «сжимаемого образца» [2]. При этом значение приращения ΔCj влияющего элемента принято 0,0045 (0,45%). Приращение поверхностной плотности на этапе расчета коэффициентов влияния 
(при фиксированном элементном составе образца) принято 0,00005 
.
Основная информация о составе и поверхностной плотности образца сравнения (ОС) и соответствующих гипотетических образцов для расчета коэффициентов межэлементных влияний приведена в табл.
Рассчитанные интенсивности флуоресценции имитировали измеренные величины для следующих экспериментальных условий: рентгеновская трубка с W-анодом, напряжение - 40 кВ, толщина бериллиевого окна 0,125 мм, углы падения и выхода излучения -φ =350, ψ=650.
Нулевое приближение для содержаний компонентов находили методом прямого внешнего стандарта
. (3)
Окончательные значения искомых содержаний Ci определяли с использованием уравнений вида (1) и метода итераций. При этом число шагов (итераций) не превышало пяти.
Диапазон изменения содержания элементов в «анализируемых» образцах 20-25% (
), 25-40 % (Ir ), диапазон изменения поверхностной плотности образцов - 0,00007 - 0,0002 .
Таблица 1.
|
Влияющий элемент |
Содержание элементов гипотетического образца после приращения содержания влияющего элемента, % |
Поверхностная плотность, г/см2 |
|||
|
Cr |
Fe |
Ni |
Ir |
||
|
Cr |
22,85 |
22,4 |
22,4 |
32,35 |
0,0001 |
|
Fe |
22,4 |
22,85 |
22,4 |
32,35 |
0,0001 |
|
NI |
22,4 |
22,4 |
22,85 |
32,35 |
0,0001 |
|
Ir |
22,4 |
22,4 |
22,4 |
32,8 |
0,0001 |
|
m |
22,5 |
22,5 |
22,5 |
32,5 |
0,00015 |
|
Образец сравнения |
22,5 |
22,5 |
22,5 |
32,5 |
0,0001 |
|
Относительная среднеквадратическая погрешность σ по данным 15 определений, % |
0,07 |
0,06 |
0,06 |
0,11 |
|
СПИСОК ЛИТЕРАТУРЫ:
- Дуймакаев Ш.И., Тарнопольский М.Г., Дуймакаева Т.Г., Шполянский А.Я. / Заводская лаборатория. 1993. №11. С. 16-19.
- Дуймакаев Ш.И., Тарнопольский М.Г., Дуймакаева Т.Г., Шполянский А.Я. / Заводская лаборатория. 1994. №4. С. 18-20.