Падение тел в поле гравитационных и диссипативных сил
Продувка различных тел в аэродинамической трубе обладает рядом недостатков [4]. Основные из них - трудности измерения скорости потока воздуха и аэродинамической силы сопротивления, действующей на тело. Эти трудности наиболее существенны при малых скоростях тела. От этих недостатков избавлен метод, основанный на изучении движения тел в поле силы тяжести при наличии диссипативной силы, которой является сила аэродинамического сопротивления. Единственное обстоятельство, которое при этом следует учитывать, заключается в следующем. Измерение зависимости времени падения тех или иных тел от пройденного расстояния не является эффективным. В этом случае мы неизбежно придем к некорректно поставленной задаче, а значит, выяснить характер зависимости силы от скорости не представится возможным. Наиболее чувствительной к характеру аэродинамического сопротивления является зависимость времени падения от массы тела. Это обусловлено тем, что масса тела, относясь к прямо измеряемым величинам, определяет скорость движения тела. Если сила сопротивления Fr пропорциональна скорости тела v
![]() , (1)
, (1)
то связь высоты падения h со временем t определяется выражением
![]() , (2)
, (2)
если же сила сопротивления пропорциональна квадрату скорости
![]() , (3)
, (3)
то зависимость высоты от времени падения есть ничто иное, как
![]() . (4)
. (4)
Следует обратить внимание, в любую связь высоты со временем коэффициент сопротивления и масса тела входят только в виде комбинаций m/λ, либо m/σ. Монотонность зависимости коэффициентов сопротивления от площади сечения, разумеется, должна сохраняться. Поэтому имеет смысл представлять экспериментальные зависимости времени падения t от массы m и площади сечения S в переменных Sβ/m.
На рис. 1 представлены результаты таких измерений при β=5/4. Измерения проводились для полых лавсановых конусов различных размеров и квадратных тонких пенопластовых платформ для значений высоты h=0.67 м и h=1 м. Точность одного измерения интервала времени не хуже 0.01 с. Такая точность измерения позволила выяснить, что сила сопротивления в динамическом режиме пропорциональна не площади, а площади в степени β≈5/4. Более того, оказалось, что падение плоских тел, какими были квадратные платформы, и конусов острием вверх описывается одной и той же зависимостью
![]() , (5)
, (5)
где k=0.14 при h=0.67м и k=0.22 при h=1м, если площадь измерена в единицах м2, масса - в кг, а время - в секундах. Здесь
![]()
время свободного падения и δ=1 для падения квадратных платформ и конусов острием вверх. Представленные на рис. 1 результаты соответствуют изменениям площадей сечения тел более чем в 5 раз, масс - в 10 раз. При этом минимальное значение площади равнялось 0.02 м2, а минимальная масса падающего тела - 0.02 кг.
Время падения конуса острием вниз, разумеется, меньше. Существенно меньшую величину должны иметь и коэффициенты сопротивления. В качестве переменной, характеризующей асимметрию тела, имеет смысл взять отношение боковой поверхности конуса Sc к площади сечения тела. Оказалось, что если
![]() , (6)
, (6)
то задержка t-t0 для конуса, падающего острием вниз, в δ раз меньше, чем для того же конуса, падающего острием вверх. Это продемонстрировано на рис. 1. Во столько же раз будут отличаться коэффициенты сопротивления. По существу, коэффициент δ есть ничто иное, как параметр асимметрии системы [7]. Максимальное значение отношения Sc/S для представленных на рис. 1 результатов составляет 2.7. Это соответствует параметру асимметрии 1.9 . Ожидалось, что эта величина будет составлять не менее 5 [4].
Зависимость силы аэродинамического сопротивления от скорости
Пока не ясно, как решить обратную задачу, то есть по экспериментальным данным (рис. 1) восстановить характер зависимости силы сопротивления от скорости тела. Поэтому имеет смысл воспользоваться достаточно простым предположением, - считать, что сила сопротивления пропорциональна vu, а показатель степени u найти из условия независимости коэффициента сопротивления от массы m и площади S. В этом случае движение тела в поле гравитационных и диссипативных сил описывается дифференциальным уравнением
![]() (7)
(7)
с нулевыми начальными условиями h(t=0)=0; dh/dt(t=0)=0. Процедура определения показателя степени u и коэффициента сопротивления a заключается в следующем. Для заданного значения u и всего набора экспериментальных значений t и параметров m, S и h определяются значения α, удовлетворяющее дифференциальному уравнению (7). Варьируя u, определяется такое его значение, при котором коэффициент сопротивления наиболее слабо зависит от массы, площади сечения и параметра асимметрии тела. Оказалось, что это происходит при u≈5/2. При этом среднее значение коэффициента сопротивления оказалось равным
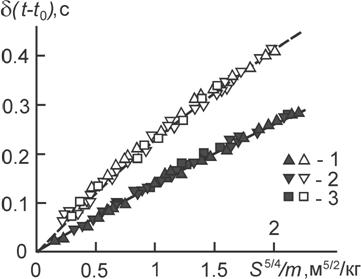
Рис. 1. Экспериментальные значения времени падения конусов (1 - острием вверх, 2 - острием вниз) и квадратных платформ (3) при различных массах и площадях сечения. Сплошная кривая и темные точки - зависимость (5) и экспериментальные данные для h=0.67м (k=0.14), штриховая кривая и светлые точки - для h=1м (k=0.22).
Независимость так определенного коэффициента сопротивления от массы и площади сечения продемонстрирована на рис. 2. На том же рисунке показаны результаты аналогичных численных расчетов с использованием эмпирической зависимости (5). Коэффициент сопротивления можно определить более точно, однако, для этого следует допустить более сложную зависимость силы аэродинамического сопротивления от площади сечения и скорости. Пока же ясно, что при малых скоростях тела сила сопротивления не пропорциональна ни площади, ни квадрату скорости. Даже параметр асимметрии в этом диапазоне скоростей оказался неожиданно мал. Итак
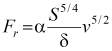 ,
,
и необходимы дополнительные экспериментальные и теоретические исследования для того, чтобы сделать эту зависимость более точной.
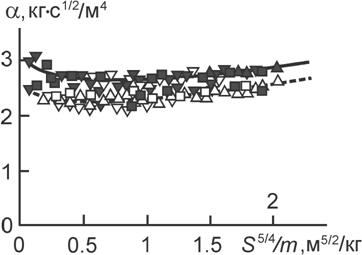
Рис. 2. Коэффициенты сопротивления. Обозначения - те же, что и на рис. 1.
СПИСОК ЛИТЕРАТУРЫ:
- Хаппель Дж., Бренер Г. Гидродинамика при малых числах Рейнольдса. М.: Мир, 1976. 632 с.
- Седов Л.И. Методы подобия и размерности в механике. М.: Наука, 1964. 428 с.
- Горлин С.М., Слезингер И.И. Аэродинамические измерения. М.: Наука, 1964. 720 с.
- Стрелков С.П. Механика. М.: Наука, 1975. 560 с.
- Герасимов С.А. О силе аэродинамического сопротивления. // Техника и технология. 2005. № 5. С. 23-26.
- Герасимов С.А. Об автомодельности аэродинамического сопротивления. // Вестник машиностроения. 2007. № 1. С. 34-35.
- Герасимов С.А. Аэродинамика зонтообразного тела с квадратичным сопротивлением движению. // Полет. 2006. № 10. С. 55-57.



