Гальваностатический режим можно представить системой уравнений (1-5). Постоянство потока ионов на границе электролит-окисел определяется уравнением (1). Изменение концентрации подвижных ионов в окисле происходит в результате диффузионного и миграционного перемещения (2). На границе окисла и металла подвижные ионы вступают в химическую реакцию (3), которая определяет увеличение толщины слоя (4). Уравнение (5) учитывает поле в диэлектрике, образованное заряженными ионами.
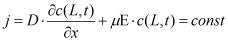 (1)
(1)
![]() (2)
(2)
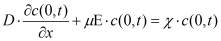 (3)
(3)
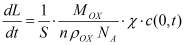 (4)
(4)
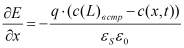 (5)
(5)
где c(x,t)- концентрация подвижных ионов, cвстр(x) - концентрация встроенного заряда на границе раздела окисел-электролит, D, μ, - соответственно коэффициент диффузии, подвижность ионов, а Ε = dφ/dx - напряженность электрического поля, χ - скорость химической реакции, MOX - молярная масса образующегося оксида, ρOX - плотность оксида, NA - число Авогадро, nox - валентность реакции образования окисла, с - концентрация подвижных ионов в окисле, свстр - равновесная концентрация заряженных ионов адсорбированных на границе окисел электролит.
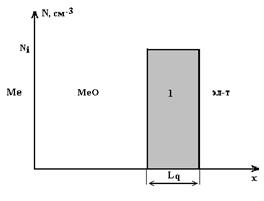
Рис. 1. Распределение встроенного заряда по глубине окисла, где Lq - ширина области с зарядом, Ni - концентрация заряженных ионов
Граничное условие постоянной плотностью потока - уравнение (1). Начальные условия (t = 0) для уравнения (1) определяются некоторой начальной концентрацией c´ (при начальной толщине окисла L =L0 ).
c(x,0) = c´ = const (L = L0 ) (6)
Была выбрана следующая форма распределения встроенного заряда по глубине диэлектрика (рис. 1).
Численный расчет кинетических зависимостей роста напряжения в процессе окисления поверхности ниобия производился на основе системы уравнений (1) - (5). В процессе моделирования из условия наилучшего согласования экспериментальной и теоретической зависимости подбирались следующие параметры: φ0 - электрохимический потенциал, Lq - глубина залегания встроенного заряда, χ - коэффициент скорости хим. реакции, cвстр - концентрация встроенных ионов.
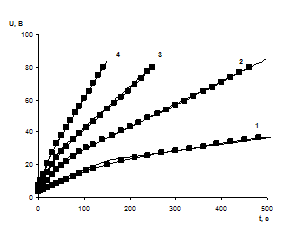
Рис.2. Теоретические и экспериментальные кинетические зависимости роста напряжения в процессе окисления поверхности ниобия. Помеченные маркером - теоретические, без маркера - экспериментальные зависимости. 1) j = 1 мА/см2, 2) j = 2 мА/см2, 3) j = 3 мА/см2, 4) j = 4 мА/см2
На рис. 2 представлены теоретические и экспериментальные кинетические зависимости роста напряжения в процессе окисления поверхности ниобия для различных значений тока реакции j. Из полученных данных следует, что экспериментальный излом графика объясняется наличием положительного заряда на границе окисел-электролит.
В зависимости от плотности тока рассчитаны следующие параметры: 1) величина и зависимость скорости химической реакции, 2) распределение и концентрация встроенного заряда, 3) изменение потенциала и напряженности поля в окисле и в области встроенного заряда.
Исследовано влияние концентрации электролита и скорости химической реакции на кинетику роста окисла. Изменение концентрации электролита сказывается на кинетике роста через встроенный на внешней границе заряд. В случае изменения состава подложки кинетика роста изменяется за счет изменения скорости реакции.
Предложенная модель процесса анодного окисления достаточно точно отражает кинетические зависимости возрастания напряжения. Объясняет зависимость кинетики роста напряжения от концентрации электролита. Подбор параметров модели позволяет определить концентрацию и распределение носителей по толщине. Концентрация ионов на границе раздела окисел - электролит логарифмически зависит от плотности тока. Это указывает на выполнение условия j = Aexp(BE). Незначительный изгиб зависимости lnj ~ E j определяется полем подвижных ионов.
СПИСОК ЛИТЕРАТУРЫ:
- Юнг Л.Анодные окисные пленки. - Л.: Энергия, 1967
- Одынец Л.Л., Орлов В.М. Анодные окисные пленки. - Ленинград, "Наука", 1990.
- Авдеев Н.А., Сиговцев Г.С. О математических моделях процессов анодного окисления. Труды петрозаводского государственного университета: сер. Прикладная математика и информатика. Вып.9./ Под.науч. ред. Проф. В. И. Чернецкого. ПетрГУ. - Петрозаводск, 2000, с 57.



