Scientific journal
Modern high technologies
ISSN 1812-7320
"Перечень" ВАК
ИФ РИНЦ = 0,940

Personal portfolio

PARALLEL CLUSTER MODELLING CHARGED PARTICLES PASSAGE IN A SOLID

A.P. Torshin P.V. Serba G.G. Chervyakov
The method of parallel cluster modeling processes of surface layer atoms carrying into solid is offered. It allows to avoid the decision of the carrying equation, describing passage of flying particles in materials with non-uniform on depth structure.
Взаимодействие быстрых ионов с твердым телом приводит к выбиванию атомов и молекул материала [1, 4]. На таком явлении сравнительного эффективного образования заряженных частиц (вторичных ионов) и основан метод легирования атомами отдачи и стимулирования процессов миграции атомов. При внедрении ускоренного иона в кристалл образуются каскады смещений, в которых происходит беспорядочное перемещение атомов. Если облучается структура, состоящая из тонкой металлической пленки, расположенной на поверхности полупроводниковой пластины, то при соответствующем выборе энергии ионов и дозы облучения происходит не только легирование атомами отдачи, но и активное перемещение атомов пленки в подложку, а атомов подложки в пленку.

Процесс миграции атомов описывается кинетическим уравнением [1]

,   (1)

где c(x,t) - относительная концентрация атомов i-го сорта на глубине x, в момент времени t, L(x,ξ) - оператор атомного смещения, U - скорость роста пленки на поверхности твердого тела, V - оператор релаксации кристаллической решетки. Граничные условия для уравнения (1) имеют вид

,                                   (2)


где S - коэффициент распыления и характеризуют баланс потоков атомов распыляемых с поверхности и мигрирующих к поверхности образца из объема твердого тела,

Функция атомного смещения L(x,ξ) описывает вероятность того, что атом, находящийся на глубине ξ, после облучения ионами будет находиться на глубине x, Для расчета функции атомного смещения необходимо знать распределение налетающих частиц по энергиям E, глубине x и направлениям движения Ω - φ(E,x,Ω), → Ω´, сечение передачи энергии от налетающих частиц атомам отдачи σ(E,Ω → T,Ω´) и функцию распределения пробегов атомов отдачи с энергией T, движущихся в направлении Ω´ G(x,T, Ω´). Функции атомного смещения может быть рассчитана по формуле

. (3)

Использование (3) для расчета функции атомного смещения сопряжено с рядом математических трудностей, прежде всего, возникают затруднения при решении уравнения переноса, описывающего прохождение налетающих частиц в материалах с неоднородным по глубине составом. Поэтому для расчета функции целесообразно использовать метод Монте-Карло. Алгоритм вычисления траектории одной частицы состоит из выполнения следующей последовательности действий:

По заданной энергии ионов находится его тормозная способность при неупругих столкновениях и рассчитываются потери энергии иона.

С помощью генератора случайных чисел разыгрывается случайное значение прицельного параметра, затем при конкретном значении прицельного параметра рассчитываются угол рассеяния в системе центра масс и энергия, переданная атома мишени.

  1. Рассчитываются углы рассеяния иона и атома отдачи в лабораторной системе координат и значения азимутальных углов.
  2. Рассчитываются значения направляющих косинусов.
  3. Определяются координаты точек взаимодействия налетающих ионов с атомами отдачи.
  4. Вычисляется энергия иона в конце шага.
  5. Вычисленная энергия проверяется на возможность обрыва траектории по энергетическому критерию или по критерию выхода иона за пределы образца. Здесь минимальная энергия, при которой ион может двигаться в кристалле.
  6. Если обрыва траектории нет, то возвращаются к пункту 1.

При моделировании траекторий смещенных атомов мишени (атомов отдачи) формируются массивы данных, содержащие информацию о координатах столкновений с налетающими ионами, энергии и направления вылета смещенных атомов. Моделирование траектории начинают для атома отдачи, имеющего наибольшее значение индекса. Фрагмент траектории атомов отдачи показан на рис. 1, где, арабские цифры (1, 2 - 6) - точки столкновений иона с атомами мишени, римские цифры - траектории. Траектория иона соответствует линии I. Линии II, III, IV соответствуют траекториям смещенных атомов мишени. Арабскими цифрами указана последовательность моделирования их траекторий. Точки n, n - 1, n - 2 - номера индексов массивов.

Рис. 1. Траектории атомов отдачи после соударения с налетающим ионом (I - траектория иона, II, III, IV траектории смещенных атомов мишени, точки n, n - 1, n - 2 - номера индексов массивов)


Для построения функции атомного смещения фиксируются стартовая позиция атома отдачи и точка его остановки, затем производя статистическую обработку, строится массив .

Кинетическое уравнение (1) может быть решено с использование численных методов. С этой целью используется дискретный аналог уравнения, который можно получить, заменив производную по времени через разностное отношение, а интеграл в правой части представляя в виде суммы

,  (4)

здесь ci,k  - концентрация атомов на глубине ih в момент времени, h - шаг дискретизации по глубине, τ - шаг дискретизации по времени,

. (5)

Разностная схема (4) не является устойчивой, поскольку с увеличением отношения τ/h2 решение уравнения будет расходиться. Для получения устойчивого решения следует использовать неявную разностную схему [3]

.   (6)

В матричной форме (6) может быть записано в виде

Ac = B,  (7)

здесь элементы матриц равны  и .

Чтобы учесть граничные условия третьего рода (2), воспользуемся дискретным аналогом

, (8)

здесь α = ISi/N. Заменив в (6) элементы первого столбца матрицы системы алгебраических уравнений элементами - (α- V)τ/h + τD/h2, будут учтены граничные условия. Таким образом, при использовании численных методов интегродифференциальное уравнение (1) с помощью метода конечных разностей приводится к системе линейных алгебраических уравнений.

Поскольку количество уравнений в системе слишком велико целесообразно использовать итерационные методы решения [2]. При этом погрешность во время поиска решения не накапливается. Последовательные приближения к решению в таких методах генерируются выполнением умножений матрицы на вектор. Итерационные методы для решения линейных систем включают следующие базовые операции линейной алгебры: линейная комбинация векторов, скалярное произведение векторов, умножение матрицы на вектор и решение систем с треугольными матрицами. При параллельной реализации таких операций производится декомпозиция данных и операций по числу используемых параллельных процессов, которая сопровождается передачей данных между процессами для обеспечения локальных вычислений.

Получая начальное приближение c(k), метод Якоби рассчитывает новое приближение к точному решению для каждой компоненты по следующей формуле:

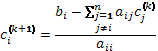,i =1,..,n, k = 0,...,                     (9)

где k - номер итерации.

Если обозначить за D диагональную матрицу, образованную диагональными элементами A, а за L и U - нижнюю и верхнюю треугольные матрицы вида

, , ,

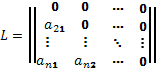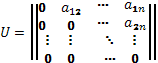то (9) можно записать как

  (10)

В качестве критерия завершения итерационного процесса можно использовать следующее условие:

.    (11)

Поскольку вычисления каждой компоненты вектора c(k) зависят лишь от значений компонент вектора, рассчитанных на предыдущей итерации, и могут выполняться одновременно, данный метод имеет высокую степень параллелизма. Рассмотрим для параллельной реализации метода Якоби следующий алгоритм. Представим исходную матрицу А в виде блоков из одинакового числа строк расширенной матрицы А. Количество блоков равно числу активированных процессов (рис. 2).

Рис. 2. Разбиение исходной матрицы A на полосы в случае 4-х процессоров

Тогда каждый процесс может вычислять фрагмент вектора c(k) в своей полосе. Количество координат вектора, которые вычисляются в каждом процессе, определяется следующим образом:

COUNT = (IAM+1)*M_SIZE/NPROC - IAM*M_SIZE/NPROC,


где COUNT - количество координат вектора, вычисляемых в данном процессе; IAM - собственный номер процесса; NPROC - количество процессов приложения; M_SIZE - размерность вектора.

Таким образом, каждый процесс может вычислять свое количество COUNT новых значений координат вектора. После этого процессы могут обменяться вновь вычисленными значениями, что позволит главному процессу произвести оценку точности вычислений.

Оценка эффективности параллельного алгоритма на основании закона Амдаля, показала, что доля параллельных операций составляет 95%. Поэтому более чем 20 кратного ускорения ожидать не следует. Практически достигаемое ускорение равно 10 при использовании 20 процессоров. Большее количество процессоров использовать нецелесообразно. Таким образом, использование параллельных вычислений для решения задач такого класса является целесообразным и эффективным.


Список литературы

  1. Блинов Ю.Ф., Серба П.В. Математическое моделирование процессов ионно-лучевого перемешивания // Микроэлектроника. 2000. № 1. -С. 59 - 63.
  2. Высокопроизводительные вычисления на кластерах. Под ред. А.В. Старченко, - Томск: Изд-во Томского университета, 2008, 198 с.
  3. Тихонов А.Н., Самарский А.А. - Уравнения математической физики. - М.: Наука, 1999. -799 с.
  4. Экштайн В. Компьютерное моделирование взаимодействия частиц с поверхностью твердого тела. - М.: Мир, 1995. - 321 с.