Метод термостимулированных токов (ТСТ) широко используется для исследования электрофизических свойств полупроводниковых и диэлектрических материалов, применяемых при изготовлении дискретных приборов и элементов интегральных схем. Данный метод привлекает исследователей своей высокой информативностью, которая сочетается со сравнительной простотой технической реализации [1].
В запрещенной зоне аморфных и стеклообразных полупроводников и диэлектриков, как правило, имеется квазинепрерывное энергетическое распределение центров захвата носителей заряда [2]. Энергетическое распределение центров захвата может иметь различную форму и определяться технологией приготовления исследуемых структур. Поэтому аналитическая интерпретация экспериментальных зависимостей ТСТ затруднена.
В данной работе при помощи математического моделирования исследуется влияние вида энергетического распределения центров захвата на адекватное описание экспериментальных зависимостей термостимулированного тока.
Математическая модель
Для математического описания процесса ТСТ была выбрана следующая система диффузионно-дрейфовых уравнений. В этой модели учитывается: термическая ионизация носителей, их дрейф и диффузия, повторный захват на ловушки и, наконец, уход через контакты. Учитывается внешнее электрическое поле и внутреннее, создаваемое заряженными носителями.
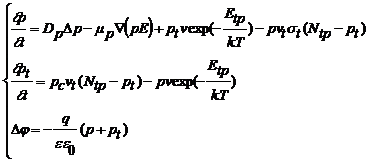 (1)
(1)
граничные и начальные условия описываются системой уравнений (2)
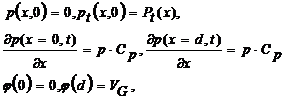 (2)
(2)
где pt - концентрация захваченных дырок, p - концентрация свободных носителей, Pt(x) - начальное распределение захваченного заряда, Ntp(x) - распределение концентрации центров захвата, μp - подвижность, Dp - коэффициент диффузии, n- частотный фактор, Vt - тепловая скорость, st - сечение захвата на ловушки, Etp - энергия активации ловушек, T(t) - зависимость абсолютной температуры от времени, φ - потенциал электрического поля, k - постоянная Больцмана, ε - диэлектрическая проницаемость окисла, ε0 - диэлектрическая проницаемость вакуума. Cp - скорость ухода дырок через контакты. В нашем случае коэффициент Сp был выбран порядка 10, что означает высокую степень проводимости контактов.
Решение системы уравнений (1) дает распределение концентрации свободных дырок и захваченного заряда по глубине диэлектрика и во времени для одного сорта моноэнергетических ловушек и позволяет рассчитать кинетические зависимости ТСТ по формуле (3).
![]() (3)
(3)
Система уравнений (1) справедлива только для моноэнергетических ловушек. В случае непрерывного энергетического спектра центров захвата введем функцию распределения ловушек по энергиям f(E) в виде функции Гаусса
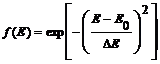 (4)
(4)
Тогда, распределение захваченного заряда по энергиям определяется формулой
N(E) = N0 × f(E) (5)
Скорость термической ионизации ловушек находится из выражения (6) Предполагается, что частотный фактор для всех ловушек один и тот же.
![]() (6)
(6)
Важным фактором при нахождении численного решения является необходимость учета изменения функции N(E) со временем, так как ловушки с малой энергией активации будут отжигаться раньше, чем ловушки с большей энергией.
Экспериментальные результаты
С помощью приведенной модели производился численный расчет ТСТ при линейной температурной развертке для оксида ниобия Nb2О5. На рис. 1. представлены экспериментальные и теоретические (расчетные) зависимости ТСТ.
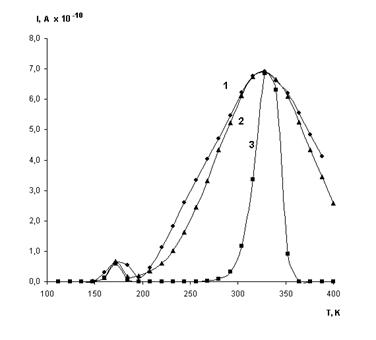
Рис. 1. Зависимость ТСТ от времени при линейной температурной развертке. 1 - экспериментальная зависимость,2 - расчетная зависимость для центров захвата с Гауссовым энергетическим распределением, 3 - для моноэнергетических центров захвата
Для расчета приняты следующие электрофизические параметры структуры:
Толщина окисла dox = 100 нм, приложенное напряжение к контактам VG = 0,5 B, диэлектрическая проницаемость εs = 3,0 , скорость линейного нагрева β = 0,5 С/сек, подвижность порядка μn = 10-9 см2/В×, коэффициент диффузии определялся из соотношения Эйнштейна.
Неизвестные параметры подбирались из условия лучшего согласия теоретической и экспериментальной зависимости. Для данной структуры они составили:
Ntp = 2,1 1017 см-3(предполагается равномерное распределение центров захвата по глубине окисла)
Еtp1 = 0,43 эВ, глубина залегания ловушек первого максимума
Еo = 0,87 эВ, расположение максимума энергетического распределения второго пика
ΔЕ = 0,18 эВ, дисперсия энергетического распределения.
При расчете зависимости ТСТ для моноэнергетических центров захвата (кривая 3) наблюдаются значительные отклонения от экспериментальной кривой. Наилучшее совпадение расчетной и экспериментальной зависимости ТСТ наблюдается для центров с Гауссовым энергетическим распределением (кривая 2). График этого распределения представлен на рис.2.
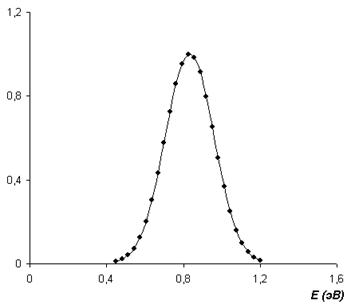
Рис. 2. Функция энергетического распределения центров захвата
Заключение
1. Предложена математическая модель ТСТ на основе диффузионно-дрейфовых уравнений переноса для центров захвата с Гауссовым энергетическим распределением.
2. Без рассмотрения в модели распределения центров захвата по энергиям не удается достичь хорошего согласия теоретических и экспериментальных данных.
3. Подобраны параметры Гауссова энергетического распределения центров захвата из условия наилучшего совпадения экспериментальной и теоретической зависимостей для оксида ниобия Nb2O5.
СПИСОК ЛИТЕРАТУРЫ:
- Гороховатский Ю.А. «Основы термодеполяризационного анализа» М.1981 г.
- Дьяконов М.Н., Замысловский М.Г., Костров Д.В. и др. В сб. Диэлектрические материалы радиотехники.- М.: Изд-во МИРЭА, 1977, с. 60-62.
- Жданок В.И. , Глазырина Т.Д., Гороховатский Ю.А. - В сб.: Электретретный эффект и электрическая релаксация.-М.: из-во МИЭМ, 1979, вып 1, с 49-59
- Лобушкин В.Н., Моргунов М.Д., Таиров В.Н и др. - В сб.: Диэлектрические материалы радиоэлектроники.-М,: Изд-во МИРЭА, 1977, с. 68-71.
- Попов В.Д. Пострадиационный эффект в ИС. Неразрушающий контроль качества ИС. Электроника: наука, технология, бизнес. 2002. № 4. С. 36-39.
- Гришаков В.В., Попов В.Д. Модель макродефекта в подзатворном оксиде кремния МОП-транзисторов. Научная сессия МИФИ-99. Сб. научн. тр. Т. 6. М.: МИФИ, 1999. С. 76-77.
- Попов В.Д., Катеринич И.И. Метод определения надежности МОП интегральных схем с применением радиационно-термической обработки. Надежность и качество. Труды междунар. симп. Пенза: Пенз. госуниверситет, 2001. С. 235-236.



