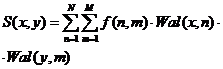Scientific journal
Modern high technologies
ISSN 1812-7320
"Перечень" ВАК
ИФ РИНЦ = 0,940

Personal portfolio

Преобразование изображений в плане улучшения качества традиционно ведется в пространственной области, где маски фильтров и алгоритмы преобразования применяются непосредственно к матрице изображения. Существуют и такой метод обработки изображения как частотный анализ. При этом осуществляется переход от непосредственно изображения f(n,m) к его спектру S(x,y), используя некоторый набор базисных функций Wal(x,y), согласно формуле

f,

где N, M - размер матрицы однократного преобразования изображения (расчет спектра может производиться за несколько шагов постоянным окном M х N). Традиционным подходом считается использование Фурье-преобразования. В статье [1] показано, что существуют преобразования, выполняющиеся за меньшее время, относительно разложения по Фурье базису, следовательно, потенциально эффективнее. К таким преобразованиям относится разложение в базисе Уолша-Адамара [2]. В данной работе будет рассмотрен метод использования частотных фильтров сглаживания изображений.

В вопросе улучшения качества, в частности сглаживания изображения, рассматривается Гауссов фильтр низких частот, передаточная функция которого для двумерного случая задается формулой

f

где D(u,v) - расстояние от начала координат обрабатываемого спектра изображения, D0 - частота среза (ширина гауссовой кривой), а также их модификации. Рассмотрим случай, когда D(u,v) задается формулой

f,

где u и v - координаты спектра изображения. Исходное изображение (а), результат (б) и срез передаточной функции фильтра (в) показаны на рисунке 1.

p

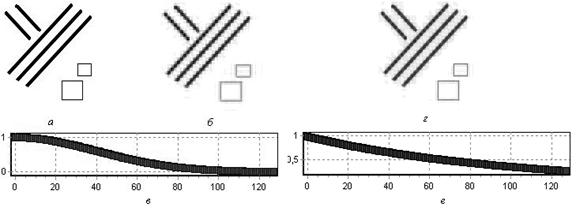
Рис. 1. Сглаживание изображения

Как видно из эксперимента, результирующее изображение (б) имеет ступенчатый размытый контур, что является особенностью использования преобразований Уолша. Эту проблему в некоторой степени удалось решить, используя фильтр, где f. Результаты приведены на рисунке 1 под буквами (г) и (е).

Проведенный анализ показывает, что использование фильтра Гаусса для анализа изображения в базисе Уолша приводит к неравномерным размытиям границ объектов, особенно при малых размерах. Однако это не снижает перспективности его использования для анализа изображений.

СПИСОК ЛИТЕРАТУРЫ:

  1. Асаев А.С., Костров Б.В., Муратов Е.Р. Сравнение трудоемкости вычислений спектров изображений Фурье и Уолша. Новые технологии в учебном процессе и производстве. Материалы третьей межвузовской научно-технической конференции. Рязань, 2005.
  2. ЗалманзонЛ.А. Преобразования Фурье, Уолша, Хаара и их применение в управлении, связи и других областях. М.: Наука, 1989. 496с.