В настоящей работе приводятся результаты расчетов вертикального распределения интенсивности звукового поля, создаваемого вертикальной линейной антенной, в изоскоростном волноводе без учета эффекта интерференции нормальных волн. В качестве волновода рассматривается однородный водный слой с постоянной скоростью звука с и плоскопараллельными абсолютно отражающими границами (поверхность абсолютно мягкая, дно абсолютно жесткое). Начало системы координат (R, Z) располагается на дне, ось z направлена вертикально вверх, толща слоя - Н. Звуковое поле создается линейной антенной апертуры L, располагающейся в волноводе вертикально с фазовым центром на горизонте Zo при R=0 и излучающей монохроматический сигнал частоты w. В предельном случае при L®0 рассматривается поле точечного ненаправленного источника. Предполагается, что антенна снабжена линейным компенсатором, позволяющим поворачивать ее диаграмму в вертикальной плоскости на заданный угол компенсации b.
Рассмотрим вначале случай точечного ненаправленного источника. Установлено, что на кривой вертикального распределения интенсивности звукового поля (при усреднении по расстоянию) имеет место максимум на горизонте излучателя Zo и минимум на горизонте Н-Zo. Впервые на это обстоятельство обращается внимание в работе [2].
Звуковое поле в водном слое будем рассматривать в виде суммы незатухающих нормальных волн. Тогда на больших расстояниях от источника интенсивность поля на горизонте z может быть записана в виде
![]() , (1)
, (1)
где к - число нормальных волн, ξ l = (k2 - bl2)1/2 и bl = (l - 0,5)p/H - горизонтальная и вертикальная компоненты волнового числа l-й нормальной волны, k = ω/C - волновое число. Пренебрежем сомножителем 1/£г. Он влияет на величины слагаемых, но не на их распределение по z. Путем простых тригонометрических преобразований это выражение может быть приведено к виду:
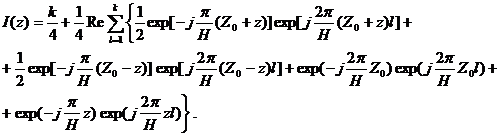 (2)
(2)
Каждый ряд в правой части этого выражения представляет собой геометрическую прогрессию и преобразуется к виду:
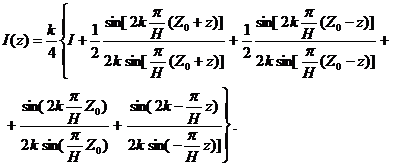 (3)
(3)
Анализ этого выражения показывает, что на кривой интенсивности I(z) имеют место следующие экстремумы. На горизонте излучения z=Zo имеет место максимум - третье слагаемое в фигурных скобках в выражении (3); на горизонте z=Н-Zo("сопряженном" горизонту излучения) имеет место минимум - второе слагаемое; на поверхности, при z=Н, на кривой I(z) имеет место минимум, а на дне, при z=0, имеет место максимум - пятое слагаемое в фигурных скобках в выражении (3).
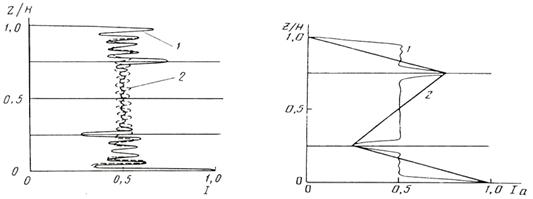
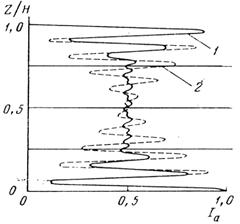
На рис. 1 представлены кривые распределения интенсивности звукового поля I(z), создаваемого точечным ненаправленным источником, помещенным на горизонте Zo=0,75Н (кривая 1) и Zo=0,5Н (кривая 2) в волноводе толщиной Н=10λ. При этом в волноводе без затухания распространяется двадцать нормальных волн: к=20. Расчеты проводились по точной формуле (1), т.е. с учетом сомножителя I/ξl1/2. На этом и последующих рисунках каждая кривая I(z) нормировалась по своему максимальному значению. На обеих кривых рис.1 на поверхности имеет место нуль, а на дне - максимум. Кроме того, на кривой 1 на горизонте излучателя Zo имеет место максимум, а на сопряженном горизонте H - Zo - минимум. Если излучатель помещается на середине водного слоя Zo=0,5H, то на этом горизонте на кривой I(z) максимум или минимум отсутствуют - сумма второго и третьего слагаемых в фигурной скобке формулы (3) равна нулю.
Обратимся теперь к случаю вертикальной линейной антенны. Излучаемое поле представляется в виде суммы нормальных волн с теми же фазовыми и групповыми скоростями, что и в случае точечного ненаправленного источника. Каждая нормальная волна в изоскоростном волноводе может быть представлена в виде суперпозиции двух плоских волн, распространяющихся вдоль волновода наклонно под углами скольжения βl=±arсsin(bl/k), а совокупность этих плоских волн образует угловой дискретный спектр в вертикальной плоскости. Угловой спектр нормальных волн, создаваемый вертикальной линейной антенной, оказывается равным угловому спектру точечного ненаправленного источника, "взвешенному" диаграммой направленности этой антенны в свободном пространстве. Таким образом, направленность вертикальной антенны в волноводе сказывается на степени возбуждения излучаемых нормальных волн.
|
Рис. 1. Распределение I(z) для точечного источника в слое: Н = 10λ, к = 20, Zo = 0,75H (кривая 1) и Zo = 0,5H (кривая 2) |
Рис. 2. Распределение Iо(z) для вертикальной линейной антенны в слое: Н = 10λ, к = 20, Zo = 0,75H, β = 0°, L = 1λ (кривая 1) и L = 5λ (кривая 2) |
Распределение интенсивности звукового поля по вертикальному сечению волновода без учета межмодовой интерференции в случае излучающей вертикальной линейной антенны будет определяться выражением
![]() (4)
(4)
где
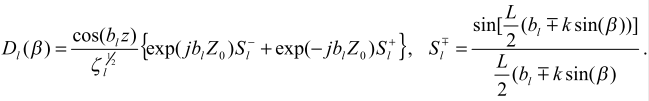
Величина Dl и (β) представляет собой ненормированную диаграмму направленности вертикальной линейной антенны в изоскоростном волноводе при излучении l-й нормальной волны. Очевидно, что при L=0 в выражении для Ia(z) (формула (4)) переходит в выражение для I(z) (формула (1)).
Если в случае точечного ненаправленного источника имеет место относительно равномерное возбуждение всех распространяющихся в волноводе нормальных волн, то в случае вертикальной линейной излучающей антенны возбуждается только часть нормальных волн. Чем больше апертура антенны, тем число возбуждаемых нормальных волн меньше. Номера возбуждаемых вертикальной антенной нормальных волн зависят от угла компенсации антенны b. При нулевом угле компенсации возбуждаются нормальные волны первых номеров, при больших углах компенсации возбуждаются нормальные волны последних номеров. При промежуточных значениях угла компенсации b возбуждаются нормальные волны средних номеров.
Рассмотрим случай нулевого угла компенсации: β = 0°. Тогда
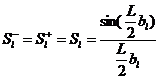 (5)
(5)
и
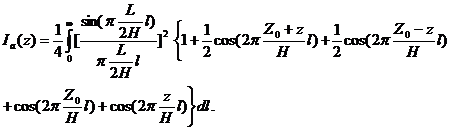 (6)
(6)
В этом случае величина Iа(z) отличается от величины I(z) (формула (1)) наличием сомножителя Sl2. Исключим в последнем выражении из рассмотрения сомножитель I/ξl1/2, а суммирование заменим на интегрирование. Проведя тригонометрические преобразования, получим
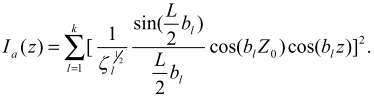 (7)
(7)
В этом выражении первый интеграл табличный, а остальные четыре представляют собой обратное преобразование Фурье от функции (SIN2X)/X2 [7]. Поэтому
![]() (8)
(8)
где
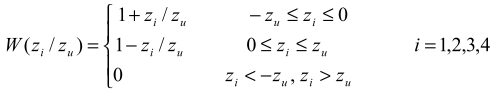 (9)
(9)
![]()
Спектр функции SIN2X/X2 есть треугольник с максимумов W(X = 0) = zu и W(X = -zu) = W(X = zu) = 0 на его границах. Таким образом, если в случае точечного ненаправленного источника экстремумы на кривой I(z) описываются функциями типа SINC, то в случае - вертикальной линейной излучающей антенны экстремумы на кривой Ia(z) описываются функциями типа равнобедренного треугольника.
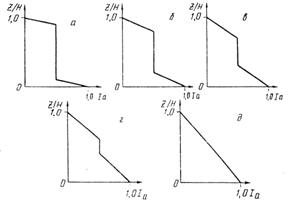
Эти результаты иллюстрируются рис.2 и 3. На рис.2 представлены кривые распределения интенсивности звукового поля Ia(z), создаваемого вертикальной антенной апертуры L = 1λ (кривая 1) и L=5λ (кривая 2) с фазовым центром на горизонте Zo=0,75H в волноводе толщиной Н=10λ. Расчеты проводились по точной формуле (6) путем суммирования и с учетом сомножителя I/ξl1/2. На рис. 3 представлены кривые Ia(z) для антенны с фазовым центром на горизонте z0=0,5H (в середине слоя) с апертурами I=2λ, 4λ, 6λ, 8λ и 10λ в том же волноводе толщины H=10λ. Из этого рисунка видно, что в случае, когда апертура антенны достигает толщины волновода L=Н, распределение Ia(z) представляет собой наклонную прямую, т.е. имеет место линейное увеличение интенсивности звука с глубиной or нуля до единицы.
В случае, когда угол компенсации β отличен от нулевого, получить такую же простую физическую интерпретацию, как в случае нулевого угла компенсации, не удается. На рис.4 представлены кривые зависимости Ia(z) интенсивности звукового поля, создаваемого вертикальной линейной антенной апертуры L=0,5λ (кривая 1) и L = 10λ (кривая 2) с фазовыми центрами на горизонтах Zo= 0,75H и 0,5H соответственно в волноводе толщиной H=10λ при угле компенсации β=30°.
|
Рис. 3. Распределение Iа(z) для вертикальной линейной антенны в слое: Н = 10λ, к = 20, Zo = 0,75H, β = 0°, L = 2λ, 4λ, 6λ, 8λ и 10λ, (рисунки а-д соответственно) |
Рис. 2. Распределение Iо(z) для вертикальной линейной антенны в слое: Н = 10λ, к = 20, Zo = 0,75H, β = 0°, L = 1λ (кривая 1) и L = 5λ (кривая 2) |
Таким образом, меняя величину апертуры линейной вертикальной излучающей антенны и положение ее фазового центра, можно подбирать различные наперед заданные распределения интенсивности звукового поля по сечению волновода. Следует отметить также, что распределение Iа(z) зависит от свойств дна и в случае, например, абсолютно мягкого дна, будет иметь совершенно другой вид.
СПИСОК ЛИТЕРАТУРЫ:
- Бреховских Л.М. Усредненное поле в подводном звуковом канале // Акуст. журн. 1965. Т. 11. № 2. С. 148-159.
- Weston D.E. Wave-theory peaks in rengeaaveraged channels of uniform sound velosity // J. Acoust. Soc. Amer. 1980. V. 68 № 1. P. 282-314.



