Расчет сопловых и диффузорных устройств до настоящего времени является сложной задачей, не имеющей однозначного аналитического решения. Все современные способы решения задач такого типа базируются, как правило, на численных методах. Основным недостатком существующих методов профилирования является необходимость задания закона изменения того или иного параметра, например, компонент скорости, давления, плотности или др., на поверхности тока [1]. Анализ известных методов профилирования показывает, что зачастую используется линейный закон изменения давления по длине канала. В отдельных случаях это соответствует действительному характеру изменения данного параметра. Выполненные на основе этого метода профили каналов при экспериментальном исследовании дают хорошие показатели. Однако при расширении диапазона варьирования давления картина резко изменяется, и канал оказывается неработоспособным: коэффициент расхода падает, возрастает уровень шума, уменьшается тяга при сопловом течении или коэффициент восстановления давления в диффузорах. Как показывают расчеты, выполненные методами термодинамики нестационарных процессов, характер изменения давления по длине канала не может быть аппроксимирован линейной функцией. В случае глубокого расширения и, особенно при сверхкритических перепадах закон изменения давления по длине канала носит ярко выраженный нелинейный характер.
Для таких условий иногда использую полиградиентные профили, однако определение такого профиля является весьма сложной задачей и по существу представляет попытку внесения субъективного фактора в объективное природное явление.
При этом изначально вводится несоответствие естественного процесса течения газа или жидкости и получаемой математической модели. При практической реализации такого канала наблюдается недорасширение или перерасширение рабочего тела при перемещении его в устройстве, имеющем профиль, не соответствующий естественному изменению параметров состояния газа. Свидетельством тому является потеря определенного количества энергии на излишнюю турбулизацию потока, создающую шумовой эффект, сопровождающий работу газодинамических каналов, - возникновение скачков уплотнения, и т.д. Известно, что за счет уменьшения отрывной зоны и увеличения неравномерности потока в минимальном сечении удается увеличить удельную тягу [2], но отсутствуют методы воздействия на эти факторы. Источником этих недостатков является отсутствие рациональных методов профилирования газодинамических каналов. Для получения работоспособного канала требуется длительная и дорогостоящая экспериментальная доводка, требующая изготовления десятков, а зачастую и сотен опытных образцов изделия.
Аналитическое решение задачи позволяет существенно сократить сроки проектирования и отказаться от дорогого процесса экспериментальной доводки, ограничившись проверкой одного опытного образца. При этом необходимо учесть, что процесс течения газа подчиняется объективным законам природы. Некоторые из этих законов еще не открыты. С целью устранения неадекватных явлений, необходимо осуществить согласование профиля канала с естественным профилем струи газа и обеспечить изменение параметров его состояния до соответствующих значений параметров среды, в которую происходит истечение.
Метод термодинамики нестационарных процессов позволяет получить адекватное аналитическое решение задачи профилирования газодинамических каналов. При таком подходе профилирование канала сводится к определению в нужном количестве последовательного ряда сечений, вычисляемых по заданным параметрам рабочего тела на входе и параметрам окружающей среды на выходе, а также к расположению этих сечений в необходимой последовательности на требуемом расстоянии друг от друга.
Первая часть задачи, заключающаяся в определении величины живого сечения канала, в настоящее время решена вполне удовлетворительно [3]. Однако при использовании традиционных методик имеет место существенная неадекватность, потребовавшая введения понятия коэффициента расхода, изменяющегося в известных пределах.
Вторая часть задачи - определение координаты расположения вычисленного сечения по длине канала - до настоящего времени не имеет рационального решения. Эмпирические правила не могут служить в общем случае основой для построения метода профилирования контура газодинамического канала, лишенного указанных выше недостатков. Методика, при которой необходимо задать: значение угла конуса, значение радиуса кривизны у входного сечения, соотношение радиуса кривизны у входного сечения с радиусом кривизны в минимальном сечении, не обладает признаками общности и применима только при возможности экспериментальной доводки проектируемого устройства. Полученный при этом профиль является однорежимным. Большие проблемы возникают в этом случае при разработке передаточных функций для регулирования профиля газодинамического канала по режимным факторам.
Таким образом, рациональный метод профилирования газодинамических каналов требует для своего построения учета, наряду с известными соотношениями, закономерности изменения параметров термодинамической системы во времени. Это позволяет представить процесс течения газа как трехмерную нестационарную задачу газовой динамики и получить некоторые частные решения аналитическим методом. Например, для случая адиабатного течения сред подчиняющихся законам идеального газа, получены выражения для определения координаты расположения вычисленного сечения по длине канала. Определяется она путем интегрирования по времени известных уравнений для нахождения скорости потока, в которых переменные параметры выражены в функции времени:
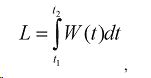
где L - расстояние по оси потока от входа в канал до текущего сечения, м;
W(t) - текущее значение скорости потока, м/с; t - время, с.
В таблице приведены размеры контура сопла прямоугольного сечения, спрофилированного по предлагаемой методике при ширине 10 мм и параметрах: p1 =0,12 МПа; Т1 =293 К; p2 =0,1 МПа.
Таблица 1
|
№ сечения |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Расстояние от входа,мм |
2 |
5 |
12 |
38 |
88 |
109 |
131 |
154 |
177 |
200 |
|
Высота, мм |
138 |
98 |
70 |
46 |
34 |
31,5 |
30 |
28,5 |
27 |
26,5 |
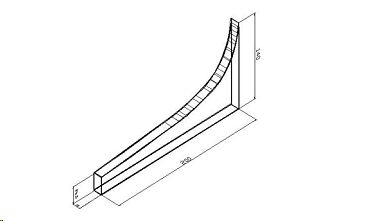
Рис.1. Вариант бесшумного сопла

Рис.2. Варианты профилей сверхзвукового сопла
На рис.1 приведен один из вариантов бесшумного сопла, изготовленного по параметрам, приведенным в табл.1. Испытания сопловых устройств, профили которых построены с помощью предлагаемого метода, проводившиеся в аэродинамической лаборатории, показали полное отсутствие шумового эффекта при истечении воздуха. При этом в ходе экспериментов было отмечено, что параметры потока не зависят от формы сечения канала. Достаточно лишь было воспроизвести закон изменения площади проходного сечения по длине при заданных начальных параметрах потока и давлении окружающей среды. В каждом сечении канала имела место неравномерность определенной структуры, обусловленная трехмерностью течения газа в процессе расширения. Исследовались каналы прямоугольного сечения с несимметричным контуром и соотношением сторон на выходе от 1х1 до 1х17. Это свидетельствует об адекватности описания полученными зависимостями реального течения газа, рассматриваемого как трехмерный нестационарный процесс (рис.1).
На рис.2 приведены варианты профилей сверхзвукового сопла, полученные при различных условиях окружающей среды.
Список литературы
- Пирумов У.Г. // Обратная задача теории сопла. М., Машиностроение, 1988. - 237с.
- Тагиров Р.К. // Определение удельной тяги на незапертых режимах и построение безотрывного контура сужающегося сопла. МЖГ, - 1990 - № 1 - 158-166 с.
- Абрамович Г.Н., //Прикладная газовая динамика, 3-е изд. - М., 1969 - 824c.



