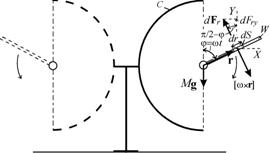
Рис. 1. Статический режим летательного аппарата c экранированным вращающимся плоским крылом.
Сначала имеет смысл рассмотреть статический режим, при котором летательный аппарат находится на поверхности (рис. 1). Это соответствует случаю, когда скорость корпуса (экрана C) равна нулю. Элемент поверхности dS крыла W, вращающегося с угловой скоростью w, испытывает действие силы сопротивления
![]() , (1)
, (1)
где ex и ey - единичные векторы вдоль осей X и Y, соответственно. Интерес, разумеется, представляет вертикальная составляющая этой силы, поэтому интегрирование (1) по площади крыла дает:
![]() , (2)
, (2)
где R - радиус крыла, S - его площадь. Эта сила отлична от нуля лишь в течении одной половины периода, поэтому средняя за период вертикальная составляющая силы сопротивления составляет существенную величину:
![]() . (3)
. (3)
Даже при коэффициенте сопротивления C, равном единице, радиусе крыла R=1 м, площади крыла S=1 м2 и частоте вращения n=10 оборотов/сек (w=2pn), (r=1,3 кг/м3 - плотность воздуха) средняя сила сопротивления (3), отождествляемая с подъемной силой в статическом режиме, составляет значительную величину Fy= 270 Н, а при десятикратном увеличении частоты вращения подъемная сила возрастает в сто раз. А это, в свою очередь, - повод для подробного изучения такого способа полета.
В динамическом режиме аэродинамическое сопротивление создается не только вращением крыла, но и движением летательного аппарата относительно воздуха. Пренебречь вторым механизмом нельзя. Это привело бы к противоречию. Действительно, в этом случае под действием сопротивления, обусловленного вращением, летательный аппарат неограниченно бы ускорялся, что привело бы к неограниченному увеличению его скорости, то есть силы сопротивления.
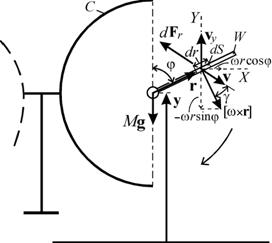
Рис. 2. Вращающееся крыло в динамическом режиме.
Итак, в динамическом режиме элемент площади крыла dS имеет две составляющие скорости vy=dy/dt и [w´r], первая из которых представляет собой скорость летательного аппарата как целого, а вторая - скорость, обусловленная вращением (рис. 2), поэтому
![]() ,
,
а сила сопротивления, действующая на этот элемент площади
![]() ,
,
приобретает вид
![]() ,
,
где γ - угол между направлением полной скорости и нормалью к поверхности крыла, то есть [w´r]. Сила аэродинамического сопротивления антипараллельна скорости [4]. Как и прежде, интерес представляет вертикальная составляющая этой силы
![]() .
.
Чтобы найти полную силу, действующую на все крыло, это выражение следует проинтегрировать по всей площади. Аналитически сделать это можно, но при этом возникает ряд проблем, связанных с записью пределов интегрирования. Поскольку речь все равно пойдет о численном решении задачи, то имеет смысл заменить интегрирование суммированием, разбив область изменения радиуса 0≤r≤R на n участков:
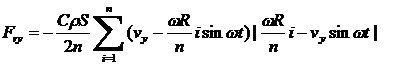 . (4)
. (4)
Понятно, что не решив уравнение движения всей системы, показанной на рис. 2, силу сопротивления (4) вычислить невозможно. Поскольку, кроме силы сопротивления (4), на систему действуют сила тяжести Mg и сила аэродинамического сопротивления корпуса летательного аппарата, то уравнение движения центра масс системы
![]() (5)
(5)
может быть переписано следующим образом:
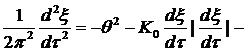
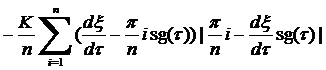 , (6)
, (6)
где
![]() . (7)
. (7)
Последняя функция отражает необходимое условие: sg(τ)=sin2πτ если sin2πτ>0, и sg(τ)=0 при sin2πτ<0.
Выше введены следующие обозначения: C0 - коэффициент аэродинамического сопротивления корпуса и
![]() , (8)
, (8)
T=2π/ω - период вращения. Эти обозначения тождественны автомодельным переменным, свойственным вибрационному перемещению так называемой летающей платформы [5]. Поэтому вполне естественно сравнить эти два способа полета. Пример такого численного расчета показан на рис. 3. Расчет проводился при C0=C и параметре асимметрии летающей платформы δ=2. Совершенно очевидно, что данный вариант полета является наиболее эффективным. Кроме того, что летательный аппарат, изображенный на рис. 1 и 2, способен поднять больший вес, он обладает еще одним положительным качеством: подавленными колебаниями корпуса. Судя по всему, интерпретация величины θ2 как приведенного веса [3,5] не является удачной. Скорее всего, величина θ представляет собой приведенный период колебаний.
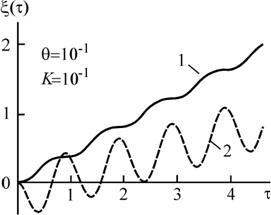
Рис. 3. Пример динамического режима ЛА с вращающимся плоским крылом (1) и летающей платформы (2).
Теперь осталось выяснить, при каких значениях приведенного коэффициента сопротивления K и приведенного периода вращения плоского крыла θ становится возможным критический режим полета, характеризующийся неизменным расстоянием от центра тяжести ЛА до земли [6]? Расчет такого режима утомителен, но не имеет принципиальных трудностей: достаточно решить трансцендентное уравнение, то есть для заданных значений K найти такие значения приведенного периода, при которых среднее значение приведенной скорости dξ/dτ равно нулю. Результаты расчета, представленные на рис. 4, не оказались неожиданными. Частота вращения, необходимая для осуществления полета ЛА с вращающимся плоским крылом, оказалась существенно ниже, чем для той же летающей платформы. Если же учесть, что больших значений параметра асимметрии в динамическом режиме достичь крайне трудно, то этот вывод можно считать достаточно общим. Попытка приравнять статическую подъемную силу (3) силе тяжести Mg приводит к следующей связи критического приведенного периода с приведенным коэффициентом сопротивления:
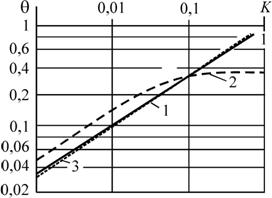
Рисунок 4. Зависимость критического периода вращения от приведенного коэффициента сопротивления для вращающегося плоского крыла (1) и летающей платформы (2). 3 - статический режим.
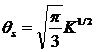 (9)
(9)
Форма корпуса на величину статической подъемной силы, разумеется, не влияет. Очень слабо влияет коэффициент сопротивления корпуса и на величину динамической подъемной силы, которая с достаточной точностью может быть аппроксимирована той же зависимостью (9).
Вывод очевиден: для легкой системы наиболее эффективным является использование вращающегося крыла. В этом случае полет достигается при меньших частотах вращения. Интересно, что при меньших приведенных коэффициентах сопротивления и прочих равных условиях летающая платформа может быть более тяжелой, но не надо забывать, что она изначально перегружена несбалансированными массами. А вообще, данная работа представляет собой редкий случай, для которого удалось вычислить статическую подъемную силу.
СПИСОК ЛИТЕРАТУРЫ:
- Блехман И.И., Джанелидзе Г.Ю. Вибрационное перемещение. - М.: Наука. 1964. - 402 с.
- Герасимов С.А. О вибрационном перемещении в поле силы тяжести. // Прикладная механика и техническая физика. 2003. Т. 44. № 6. С. 44-48.
- Герасимов С.А. Об определении подъемной силы вибрационного летательного аппарата. // Техника и технология. 2005. № 6. С. 128-132.
- Стрелков С.П. Механика. - М.: Наука. 1975. 560 с.
- Герасимов С.А. Летающая платформа с квадратичным сопротивлением движению. // Известия вузов. Машиностроение. 2005. № 10. С. 3-7.
- 6. Герасимов С.А., Удалова Е.С. Негармонический осциллятор в поле гравитационных и диссипативных сил. // Вопросы прикладной физики. 2005. № 12. С. 126-128.



