Одним из наиболее распространенных промышленных методов изготовления газонаполненных термопластичных материалов является одношнековая экструзия в двух последовательно соединенных аппаратах, что обусловлено низкими капиталовложениями и простотой организации производства по сравнению с методом двухшнековой экструзии. В первом экструдере осуществляется нагрев, плавление термопласта и смешение под давлением расплава с жидким вспенивающим агентом (как правило, изопентаном или фреоном), который растворяется в расплаве, а во втором - охлаждение и продавливание смеси через головку соответствующей конфигурации (например, плоскощелевую при изготовлении пеноплит). При выходе смеси из головки вследствие снижения давления пеноагент закипает и вспенивает твердеющий пластично-вязкий материал изнутри, образуя ячейки [1]. При охлаждении смеси за счет теплоотдачи в охлаждаемый маслом корпус и шнек ее вязкость увеличивается, вследствие чего развивается давление. Поэтому температурный профиль во втором экструдере должен быть таким, чтобы давление было достаточным для сохранения пеноагента в жидком состоянии, потому что образование пузырей пара в канале шнека приводит к повышению плотности пеноматериала. Так как температура и вязкость на производстве не измеряются, актуальной является разработка физически обоснованной экономичной модели для расчета этих показателей и поиска геометрических и режимных параметров второго экструдера, обеспечивающих их требуемые значения при перенастройке на новый тип термопласта, пеноагента и (или) производительность.
При построении математической модели процесса охлаждения приняты следующие основные допущения, строго обоснованные в литературе по моделированию экструдеров [1, 3]:
- шнек неподвижен, а корпус вращается в обратном направлении, канал шнека разворачивается на плоскость;
- течение является установившимся во времени и по длине канала z, радиальный поток отсутствует, скорости циркуляционного vx и поступательного vz потоков не изменяются по ширине x, инерционные и массовые силы малы по сравнению с силами трения;
- профиль температуры T развит по ширине, теплопроводность по длине мала по сравнению с теплопроводностью по глубине;
- на стенках канала выполняются условия прилипания смеси;
- плотность ρ, удельная теплоемкость cP и теплопроводность λ смеси выражаются через соответствующие характеристики ее компонентов - расплава (индекс m) и пеноагента (индекс b), которые не зависят от давления P и температуры в экструдере:
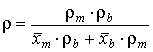 ,
,![]() ,
,![]() , (1)
, (1)
где ![]() ,
, ![]() - массовые доли компонентов, выражаемые их расходы
- массовые доли компонентов, выражаемые их расходы
![]() ,
,![]() ; (2)
; (2)
смесь расплава термопласта и вспенивающего агента является неупругим псевдопластичным материалом, реологическое поведение которого описывается моделью Оствальда-де´Вилье:
![]() ,
,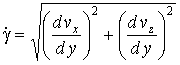 , (3)
, (3)
где η - эффективная вязкость, Па×с; μ0, b, n - эмпирические коэффициенты, зависящие от состава смеси;γ· - скорость деформации сдвига, 1/с; y - координата по глубине канала (0 ≤ y ≤ H), м.
Значения коэффициентов уравнения (3) для смесей полистирола и полиэтилена с галогеноалканами рассчитаны в работе [4] путем обработки экспериментальных данных капиллярной вискозиметрии, полученных в [5], методом наименьших квадратов.
С учетом указанных допущений структура модели охлаждения, построенной на основе законов сохранения, имеет вид:
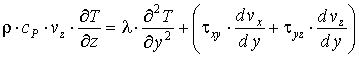 , (4)
, (4)
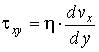 ,
,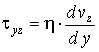 , (5)
, (5)
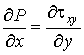 ,
,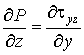 , (6)
, (6)
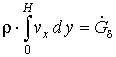 ,
, 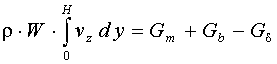 , (7)
, (7)
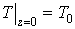 ,
,![]() , (8)
, (8)
![]() ,
,![]() ,
,![]() , (9)
, (9)
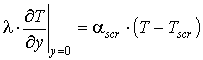 ,
,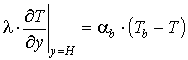 , (10)
, (10)
где τxy, τyz - напряжения сдвига в потоках, Па;G·δ - интенсивность потока утечки через зазор между корпусом и нарезкой шнека, кг/(м×с); W - ширина канала, м; Gd - расход утечки, кг/с; T0, P0 - температура (°С) и давление (Па) смеси на входе во второй экструдер; αscr, αb - коэффициенты теплоотдачи от смеси в шнек и корпус, Вт/(м2×°С); Tscr, Tb - температуры шнека и корпуса, °С.
Компоненты скорости корпуса рассчитываются по формулам:
![]() ,
,![]() , (11)
, (11)
где D - диаметр шнека, м; δ - радиальный зазор, м; N - частота вращения шнека, об/с; φ - угол наклона нарезки шнека, рад.
Вследствие существования циркуляционного потока разброс температуры относительно среднего значения в каждом поперечном сечении канала мал, поэтому можно осреднить уравнение теплового баланса (4) по глубине канала:
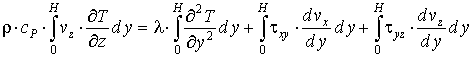 . (12)
. (12)
Слагаемые уравнения (12) преобразуются к виду:
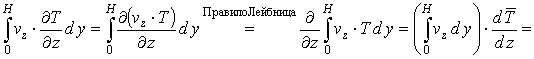
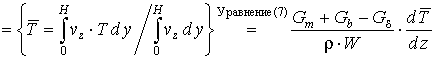 , (13)
, (13)
где T¯ - средняя по глубине канала температура смеси, °С;
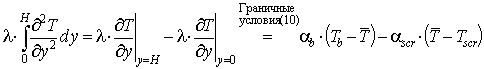 ; (14)
; (14)
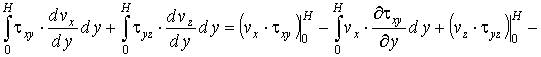
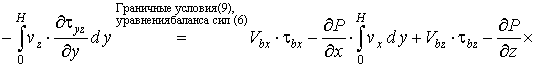
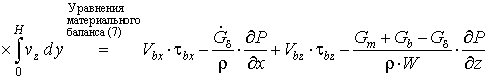 , (15)
, (15)
где τbx, τbz - напряжения в смеси у поверхности корпуса, Па.
Подстановка выражений (13)-(15) в уравнение (12) позволяет получить уравнение притока тепла на участке канала длиной dz:
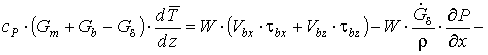
![]() . (16)
. (16)
Уравнение (16) определяет источники изменения энтальпии смеси на участке канала dz в единицу времени: приток тепла за счет диссипации механической энергии и стоки тепла за счет потока утечки, генерации давления и теплоотдачи в корпус и шнек.
Для расчета напряжений и градиентов давления используются формулы, полученные путем интегрирования уравнений (6) по координате y с учетом того, что в потоках вследствие изменения направления движения существуют сечения нулевых напряжений y0x и y0z, и перехода к безразмерным переменным [2, 3]:
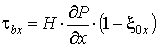 ,
,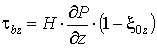 ,
,![]() ,
,![]() , (17)
, (17)
![]() ,
,![]() , (18)
, (18)
где n - отношение градиентов давления в потоках; Bz - безразмерный градиент давления в поступательном потоке; (δP/δz)N - нормирующий градиент давления, при котором y0z = 0:
![]() . (19)
. (19)
Кинематические характеристики (ξ0x, ξ0z, n, Bz) вычисляются путем решения системы нелинейных определяющих уравнений, построенной в работе [2] на базе теории плоских потоков.
Расчет утечки осуществляется по модели, построенной с учетом того, что в узком пространстве радиального зазора преобладает составляющая чисто сдвигового (вынужденного) потока в направлении окружной скорости шнека, а интенсивность утечки медленно изменяется в пределах полного витка нарезки шнека:
![]() ,
,![]() . (20)
. (20)
Подстановка выражений (17)-(20) в уравнение (16) позволяет получить окончательный вид уравнения теплового баланса:
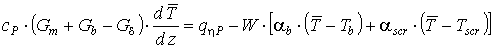 , (21)
, (21)
где qhP - удельная мощность работы сил трения и давления, равная
![]() , (22)
, (22)
![]()
![]() . (23)
. (23)
Разделение переменных в уравнении (21) с учетом (22) и введение переменной ![]() приводит к уравнению:
приводит к уравнению:
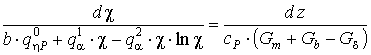 , (24)
, (24)
![]() ,
,![]() . (25)
. (25)
Интегрирование левой части уравнения (24) в пределах от χ0 до χ, а правой части - от 0 до z с учетом формулы разложения
![]() , (26)
, (26)
справедливой, так как χ >> 0,5, потенцирование полученного выражения и подстановка результата в формулу для χ дают формулы для расчета распределения температуры смеси по длине канала:
![]() , (27)
, (27)
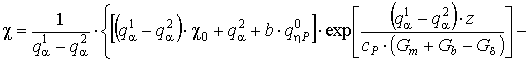
![]() , . (28)
, . (28)
Из формул (18) и (19) с учетом начального условия (8) следует формула для расчета распределения давления по длине канала:
![]() . (29)
. (29)
Аналитическая модель охлаждения смеси расплава термопласта и пеноагента в экструдере представляет собой совокупность формул (1), (2), (11), (20), (23), (25), (27)-(29), позволяющих рассчитать профили температуры и давления по длине канала шнека в зависимости от характеристик экструдера, термопласта и пеноагента. Расчет вязкости осуществляется по формулам (3) с использованием осредненной по глубине канала скорости сдвига. Модель настраивается на переменную глубину канала, поскольку часто шнек состоит из секции с увеличивающейся глубиной, за которой следует короткая суживающая секция, необходимая для предотвращения образования паровых пузырей. В этом случае кинематические характеристики вычисляются на каждом шаге по длине. Модель позволяет учесть профиль температуры корпуса Tb = f(z).
Рассчитанные профили температуры смеси расплава полиэтилена низкой плотности ( x¯m = 0,9) и дихлордифторметана ( x¯b = 0,1) в экструдере диаметром 0,15 м и глубиной канала 0,016 м при температурах корпуса и шнека, равных 110 °С, приведены на рис. 1.
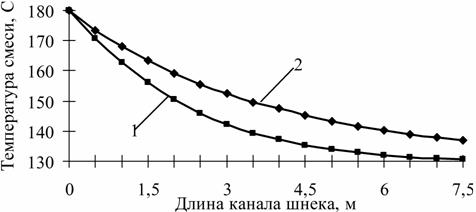
Рис. 1. Профили температуры при N = 0,3 об/с (1) и N = 0,5 об/с (2)
С ростом частоты вращения шнека температура смеси увеличивается вследствие уменьшения времени пребывания в экструдере (времени охлаждения) и повышения интенсивности диссипативных тепловыделений, обусловленных работой сил трения.
Таким образом, разработана аналитическая модель процесса охлаждения при экструзии смесей расплавов термопластов и пеноагентов, настраиваемая на состав смеси, учитывающая аномалию вязкости, тепло, выделяющееся в результате внутреннего трения, и позволяющая решить задачи исследования и выбора конструктивно-технологических характеристик одношнековых экструдеров многоассортиментных производств пеноматериалов.
СПИСОК ЛИТЕРАТУРЫ
- Берлин А.А., Шутов Ф.А. Химия и технология газонаполненных высокополимеров. - М.: Наука, 1980. - 504 с.
- Полосин А.Н. // Информационные технологии моделирования и управления. - 2007. - № 3. - С. 376.
- Торнер Р.В. Теоретические основы переработки полимеров (механика процессов). - М.: Химия, 1977. - 464 с.
- Han C.D. // Polym. Eng. Sci. - 1988. - Vol. 28, № 19. - P. 1227.
- Han C.D., Ma C.Y. // J. Appl. Polym. Sci. - 1983. - Vol. 28. - P. 831.



