При известных допускаемых нормальных напряжениях для материала рассматриваемой балки могут проводиться три варианта расчетов:
- если заданы нагрузки и размеры сечений балки, то поводится проверочный расчет на прочность;
- если заданы нагрузки, то могут быть определены размеры сечений стержня (проектировочный расчет);
- если заданы размеры сечений, то могут быть определены допускаемые нагрузки.
В каждом из трех видов задач необходимо задать исходные данные (нагрузки и длины участков). Для наглядности на рабочий лист помещается изображение расчетной схемы (рис. 1). Для проверочного расчета на прочность сначала определяются опорные реакции Ra и Rb из сумм моментов, относительно опор А и В.
После определения опорных реакций заполняется таблица с расчетными значениями поперечной силы Qy и изгибающим моментом Mz. В первом столбце указывается расстояние сечения от левого края балки в метрах с шагом 0,1 м. Полученные для двух участков балки уравнения Qy сводятся в одну формулу, которая выглядит в таблице Excel в ячейке В24 следующим образом:
=ЕСЛИ(A24<=$D$11;-$D$13*A24+$B$19;-$D$13*$D$11+$B$19-$D$14)
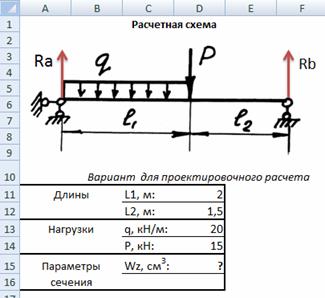
Рис. 1. Исходные данные для проектировочного расчета балки
В формуле используется функция «ЕСЛИ» для определения участка для которого указан x в ячейке А24.
Уравнения Mz сводятся в одну формулу, которая выглядит в таблице Excel в ячейке С24 следующим образом:
=ЕСЛИ(A24<=$D$11;-$D$13*A24^2/2+$B$19*A24;-$D$13*$D$11*
(A24-$D$11/2)+$B$19*A24-$D$14*(A24-$D$11))
В формулах жирностью выделено значение х.
По табличным данным строится диаграмма, на которой будет две линии (рис. 2). Первая - эпюра Qy, вторая - эпюра Mz.
При проектировочном расчете необходимо найти момент сопротивления сечения Wz. Его значение зависит от максимального изгибающего момента Mz, которое может быть определено с помощью функции Excel с названием «Поиск решения». Для расчета необходимо в одну ячейку вписать начальное приближение расстояния х (например, 1 м), а во вторую - формулу Mz, в которую подставляется х из предыдущей ячейки. Затем запускается «Поиск решения» и выполняется поиск максимального Mz (рис. 3), который можно использовать в дальнейшем расчете (Mz max = 30,63 кНм).
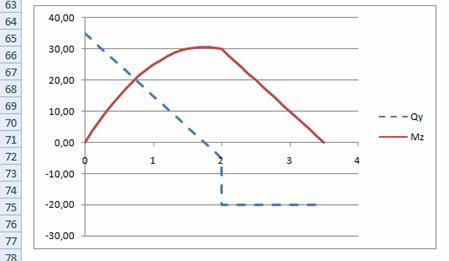
Рис. 2. Эпюры Qy и Mz на диаграмме в Microsoft Excel
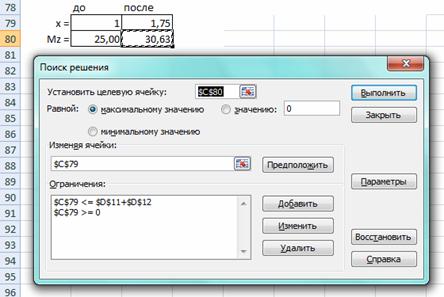
Рис. 3. Определение максимального изгибающего момента Mz
В ограничения указаны пределы изменения х (от 0 до L1 + L2).
Для расчета допускаемых нагрузок используется четыре ячейки, к вышеуказанным двум добавляется искомая нагрузка и величина нормальных напряжений σ (рис. 4). По итогам расчетов получаем q = 107,92 кН/м.
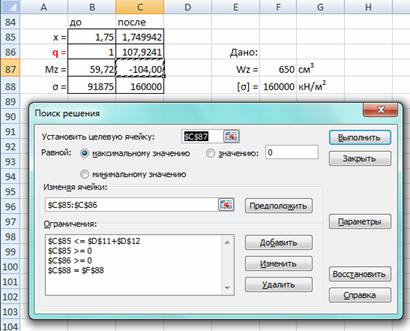
Рис. 4. Определение допускаемой нагрузки q при известном Wz
Первая и вторая строка ограничений - пределы изменения х. Третья строка - q ≥ 0. Четвертая - нормальные напряжения равны допускаемым (заданным) нормальным напряжениям для материала балки.



