Так как большая часть заготовляемого зерна поступает, как правило, с повышенной влажностью, его сохранность в процессе длительного хранения, без снижения продовольственных характеристик, во многом зависит от работы зерносушильных установок.
Большинство сельскохозяйственных предприятий агропромышленного комплекса испытывают дефицит в эффективной зерносушильной технике и не в состоянии, в ряде случаев, довести зерно до базисной товарной кондиции.
Тепло- и влагоперенос при сушке зерна подчиняется общим законам тепло- и массопереноса и является его частным случаем. Теоретической основой для них служит единая теория тепло- и массопереноса. На основе этой теории процессы переноса теплоты и влаги в зерне могут быть описаны аналитически. Такое описание позволяет определить температуру и влагосодержание в любой точке зерна или зернового слоя в любой момент времени, найти их градиенты и изменение во времени, рассчитать плотность потоков теплоты и влаги, прогнозировать дальнейшее развитие этих процессов. Вместе с тем при математическом описании процессов в зерне и зерновом слое возникают определенные трудности, так как зерно неоднородно по структуре и составу. Вследствие этого различные участки зерна имеют разную проводимость и обладают анизотропными свойствами, т. е. разной проводимостью в разных направлениях.
Зерно имеет сложную геометрическую форму, а зерновой слой представляет собой дисперсную среду, в которой зерновки ориентированы в пространстве произвольно. Кроме того, процессы переноса теплоты и влаги внутри зерна взаимосвязаны и взаимно влияют один на другой, а теплофизические и влагообменные свойства зерна зависят от его влажности и температуры, вследствие чего дифференциальные уравнения тепло- и влагопереноса носят нелинейный характер.
В основу математического описания процесса сушки зерна положена математическая модель, предложенная В. И. Жидко и А. С. Бомко, в которой пренебрегается потоками тепла в слое за счет теплопроводности в сравнении с конвективными потоками, не учитывается усадка и градиент давления.
При рассмотрении шахтной зерносушилки с подвижным слоем зерна, некоторые величины, входящие в модель, известны (толщина слоя, температура и относительная влажность сушильного агента, начальная влажность зерна и др.). Поэтому при моделировании были предварительно усреднены управляемые переменные по некоторым пространственным координатам. Пространственное распределение полей температур и влагосодержаний рассматривалось в системе координат (x, r), где x - координата по длине сушилки, м; r - координата вдоль радиуса зерна, м, при следующих допущениях: форма поверхности частицы представлена в виде неограниченного цилиндра; пренебрегалось аксиальной влагопроводностью, термодиффузией, теплопроводностью зерновой массы. Тогда математическая модель процесса сушки зерна, движущегося непрерывным потоком, представлялась в виде системы уравнений, связывающих температуру θ и влагосодержание u дисперсного материала:
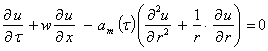 , (1)
, (1)
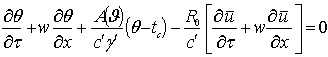 , (2)
, (2)
где
![]() , (3)
, (3)
с граничными условиями
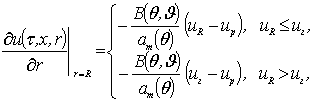 (4)
(4)
с начальными условиями
![]()
![]() ,
,
(5)
и условиями симметрии
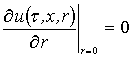 ,
,
![]() . (6)
. (6)
В уравнениях (1)-(6) приняты следующие обозначения:τ - время, с; w - скорость движения материале в аппарате, м/с; u - скорость сушильного агента на входе а зерновую массу, м/с; am - коэффициент диффузии влаги, м2/с; tc - температура сушильного агента, оС; c - теплоемкость зерновой массы, кДж/(кг×К); ρнас - насыпная плотность зернового слоя, кг/м3;ρо - плотность сухой зерновой массы, кг/м3; Ro - удельная теплота парообразования, кДж/кг; A - эмпирический коэффициент теплообмена, кДж/(м3×К); В - эмпирический коэффициент массообмена, м/с;p ,г, R - индексы соответствующие равновесному, гигроскопическому влагосодержанию и влагосодержанию на поверхности зерна.
Система (1)-(6) описывает процесс сушки дисперсного слоя при наличии поперечного движения плотного слоя при условии перекрестного движения зерна и агента сушки.
Система уравнений (1)-(6) была преобразована в безразмерную форму:
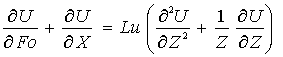 ; (7)
; (7)
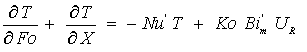 , (8)
, (8)
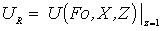 ;
;
с граничным условием для случая ![]()
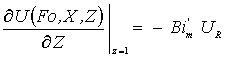 ; (9)
; (9)
с начальными условиями
![]() ,
,
![]() (10)
(10)
и условиям симметрии
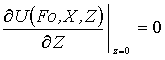 , (11)
, (11)
где 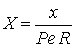 ,
, ![]() - безразмерные координаты;
- безразмерные координаты;![]() - критерий Пекле;
- критерий Пекле;![]() - коэффициент температуропроводности, м2/с;
- коэффициент температуропроводности, м2/с;![]() - безразмерная температура;
- безразмерная температура;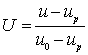 - безразмерное влагосодержание;
- безразмерное влагосодержание;![]() - критерий Фурье;
- критерий Фурье;![]() - критерий Лыкова;
- критерий Лыкова;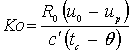 - критерий Коссовича;
- критерий Коссовича; 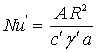 - эмпирический критерий Нуссельта;
- эмпирический критерий Нуссельта;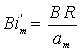 - эмпирический массообменный критерий Био.
- эмпирический массообменный критерий Био.
Таким образом, получена система уравнений (9)-(11) в безразмерном виде, описывающая процесс сушки при продольном перемещении продукта и перекрестным движением агента сушки через слой зерновой массы.
Данная система уравнений является упрощенной (не учитываются температурные градиенты, термодиффузия, распределенность источника теплоты в самой частице), но она достаточно сложна для аналитического исследования (в силу нелинейности) и может быть решена лишь приближенными вычислительными методами. При практическом построении модели конкретного объекта не обязательно знание всех теплофизических коэффициентов, входящих в модель, т. к. с помощью приближенных методов можно производить настройку модели, основываясь только на безразмерной форме ее уравнений, что, в свою очередь, предоставляет возможность идентифицировать параметры уравнений. При последующей конкретизации системы уравнений (9) - (11) применительно к существующим сушильным установкам с подвижным слоем дисперсного материала можно осуществить построение математической модели процесса сушки, необходимой для отыскания оптимальных технологических режимов и управления процессом с использованием ЭВМ.



