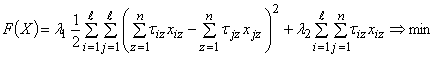, обеспечивающий минимум целевой функции:
(1)
при следующих ограничениях:
, (2)
. (3)
Элементы xiz плана распределения X являются непрерывными величинами и имеют следующий смысл: если xiz=1, то z-е задание выполняется на i-м компьютере, если xiz=0, то z-е задание на i-м компьютере не выполняется. Величина τiz - это время выполнения z-го задания на i-м компьютере,λ1 ,λ2 - коэффициенты целевой функции. Целевая функция (1) является сверткой двух критериев: загруженность компьютеров должна быть равномерной, суммарное время работы компьютеров должно быть минимальным.
Ограничение (2) требует, чтобы каждое задание выполнялось только на одном компьютере. Ограничение (3) требует, чтобы на -м компьютере задание либо выполнялось целиком, либо вовсе не выполнялось.
Задача (1)-(3) является непрерывной с ограничениями типа равенств и относится к классу задач нелинейного программирования. Для решения исходной задачи она формулируется как задача безусловной оптимизации, и в результате математическая модель распределения заданий в мультипроцессорной системе выглядит следующим образом:
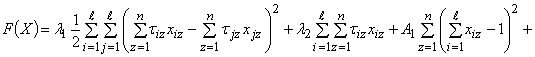
(4)
Решение имеет смысл только тогда, когда элементы вектора X принимают значения 0 или 1, поэтому решение округляется в соответствии со следующим правилом:
. 
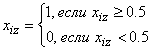(5)
Для решения задачи (4) применяется метод Флетчера-Ривса [2], который относится к классу градиентных методов поиска приближенного решения. Метод Флетчера-Ривса состоит в построении последовательности точек {Xk}, где 
,k=0,1,..., обеспечивающей убывание целевой функции (т.е. 
), где точки последовательности вычисляются по правилу:
,k=0,1..., (6)
а величина шага tk определяется для каждого значения k из условия:
. (7)
Решение задачи (7) сводится к нахождению корней полинома третьей степени. Направление убывания 
определяется по формуле:
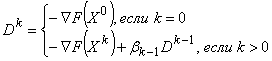, (8)
где вектор-градиент 
целевой функции и коэффициент 
определяются как:
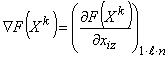и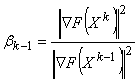 
.
Евклидова норма 
вычисляется по формуле:
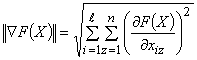(9)
Алгоритм Флетчера-Ривса состоит из следующих этапов:
Входные параметры алгоритма: начальное состояние 
, параметры критериев останова 
, предельное число итераций M.
- Установить счетчик итераций:k=0 .
- Вычислить градиент
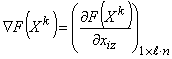, используя следующую формулу:
.
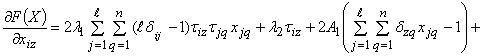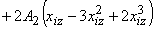
- Проверить выполнение условия окончания
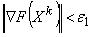. Если условие выполнено, то принять 
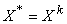и перейти на п.9. - Если выполняется условие k≤M, то X* = Xk и перейти на п.9.
- Определить направление убывания 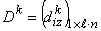по формуле (8).
- Найти
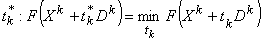. Если t*k не найден, то принять t*k = 0. - Вычислить новую точку
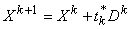. - Если одновременно выполняются условия
,
,
,
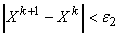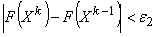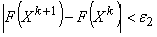, то принять X* =X k+1 и перейти на п.9. Иначе установить k = k+1 и перейти на п.2. - Округлить координаты точки
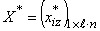в соответствии с правилом (5). - Если план X*удовлетворяет ограничениям (2) и (3), то X* - найденное решение, в противном случае - решения не найдено.
- Выход.
В работе исследовано влияние параметров алгоритма на получаемые решения и скорость работы алгоритма. Предложен способ выбора начальных точек из окрестности центра единичного куба, т.е. 
. Численные эксперименты показали, что наилучшие значения Δx находятся в интервале от 0.05 до 0.2. Однако, при слишком малом Δx может возникнуть ситуация когда все точки из окрестности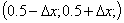 
будут находиться в области притяжения локальных минимумов, далеких от оптимального решения, что ограничит потенциальную возможность алгоритма найти глобальный минимум. Поэтому рекомендуется выбирать параметр Δx из диапазона [0.15;0.2].
В работе исследованы критерии останова и выявлены их недостатки, приводящие к избыточному числу итераций алгоритма. Предложен модифицированный критерий останова, использующий относительные приращения целевой функции, позволяющий сократить число итераций без потери качества получаемых решений.
Результаты численных экспериментов показали эффективность метода Флетчера-Ривса для решения задачи распределения заданий в мультипроцессорной системе, и были даны рекомендации по выбору параметров алгоритма.
СПИСОК ЛИТЕРАТУРЫ:
- Дегтярев Ю.И. Исследование операций: Учеб. для вузов по спец. АСУ. - М.: Высш. шк., 1986. - 320 с.: ил.
- Летова Т.А., Пантелеев А.В. Экстремум функций в примерах и задачах: Учебное пособие. - М.: Изд-во МАИ, 1998.-376 с.: ил.