Scientific journal
Modern high technologies
ISSN 1812-7320
"Перечень" ВАК
ИФ РИНЦ = 0,940

Personal portfolio

В настоящее время активно разрабатываются и внедряются распределенные информационные системы автоматизации деятельности специалистов различных предприятий и структур. В таких системах возникает необходимость решения множества аналитических задач, и от того, насколько система справится с ними, зависит быстродействие всей системы, а также оперативность принятия управленческих и финансовых решений. В связи с этим актуальной является задача распределения заданий в мультипроцессорной системе.

Математическая постановка задача выглядит следующим образом.

Пусть  - план распределения заданий, где l - число компьютеров в мультипроцессорной системе, n - число заданий,

Необходимо найти план распределения заданий, обеспечивающий минимум целевой функции:

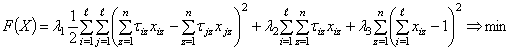, (1)

где  - весовые коэффициенты целевых и штрафной функций.

NP-полнота задачи (1) обуславливает применение приближенных методов поиска решения, среди которых хорошо зарекомендовали себя методы решения на основе нейронных сетей [1]. Нейросетевые методы характеризуются высокой скоростью получения результата и возможностью распараллеливания вычислительного процесса, но они являются методами поиска локального минимума, поэтому для нахождения глобального решения алгоритм решения необходимо запускать многократно из различных начальных состояний и выбирать наилучшее по качеству решение. В качестве начальных состояний нейронной сети предлагается использовать промежуточные результаты метода имитации отжига, который зарекомендовал себя как эффективный метод поиска глобального решения [1, 2]. Суть предлагаемого комбинированного метода состоит в следующем: реализуется алгоритм имитации отжига на основе стохастической асинхронной дискретной сети Хопфилда (САДСХ), но, в дополнение к нему, из промежуточных состояний запускается детерминированная асинхронная дискретная сеть Хопфилда (АДСХ), которая обеспечивает быстрое нахождение локального минимума целевой функции. Из найденных АДСХ решений выбирается наилучшее. Работу комбинированного алгоритма иллюстрирует рис. 1.

 

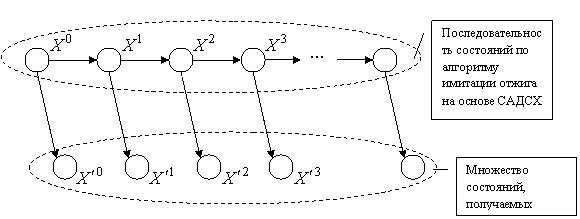
Рис. 1. Комбинированный алгоритм

Комбинированный алгоритм состоит из следующих этапов:

Входные параметры алгоритма:

  • начальное состояние ,
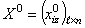  • начальная температура ,
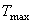  • коэффициент охлаждения ,
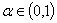  • число итераций m.
  • 1. Задать начальное состояние сети X=X0, начальную температуру T = Tmax, значение целевой функции Fmin = ∞.
  • 2. Задать признаки улучшения значения целевой функции .
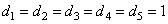  • 3. Задать номер нейрона: i=1,z=1 .
  • 4. Если 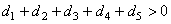, то:
  • 4.1. Задать признак d=0.
  • 4.2. Установить счетчик итераций k=1.
  • 4.3. Вычислить вероятность piz нахождения нейрона (i,z) в состоянии 1 по формул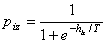е , где 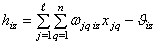- взвешенная сумма входов нейрона, 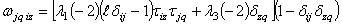- синаптический вес связи между нейронами, 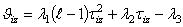- порог активизации нейрона.
  • 4.4. В соответствии с равномерным законом распределения случайных величин сгенерировать число R из диапазона (0,1).
  • 4.5. Если R<piz, то принять xiz=1, иначе xiz=0.
  • 4.6. Запустить АДСХ из начального состояния 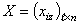, в результате чего сеть сходится к локальному минимуму .
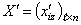  • 4.7. Если состояние 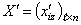 является допустимым планом распределения заданий и 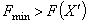, где F(X´) вычисляется по формуле (1), то присвоить 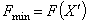, 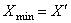и установить признак уменьшения целевой функции d=1.
  • 4.8. Если z<n, то установить  z=z+1 и перейти на пункт 4.10.
  • 4.9. Если z=n, то:
  • 4.9.1. Если i<l, то установить i=i+1, z=1 и перейти на пункт 4.10.
  • 4.9.2. Если i=l, то установить i=1, z=1 и перейти на пункт 4.10.
  • 4.10. Если k<m, то k=k+1 и перейти на пункт 4.3.
  • 4.11. Переустановить признаки уменьшения целевой функции d1=d2, d2=d3, d3=d4, d4=d5, d5=d.
  • 4.12. Вычислить новую температуру  T = α * t и перейти на пункт 4.
  • 5. Если Fmin ≠ ∞, то 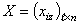- полученное решение, иначе - решения не найдено.
  • 6. Выход.

Трудоемкость разработанного алгоритма оценивается как 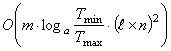, где α - коэффициент охлаждения, m - количество итераций при постоянной температуре, Tmax - начальная температура отжига, Tmin - конечная температура, при которой отжиг прекращается.

Экспериментальные исследования комбинированного алгоритма, алгоритма решения на основе дискретной сети Хопфилда и алгоритма имитации отжига на основе стохастической сети Хопфилда показали, что комбинированный алгоритм находит наилучшие решения среди рассматриваемых алгоритмов.

Использование в комбинированном алгоритме нейронных сетей позволяет легко распараллелить вычислительный процесс, что приведет к существенному увеличению скорости получения решения при использовании компьютеров с многоядерными процессорами или при решении данной задачи на кластерах.

 

СПИСОК ЛИТЕРАТУРЫ:

  1. Уоссермен Ф., «Нейрокомпьютерная техника» - М.: Мир, 1992. - 240 с.
  2. Kirkpatrick S., Gelatt C.D., Vecchi M.P. Optimization by simulated annealing / Science. Vol. 220, Number 4598, May 13, 1983, p. 671-680.