Изучению характеристик мод Лэмба, распространяющихся в пьезокристаллических пластинах посвящено достаточно много работ [1-3]. Показано, что квазипоперечные SH моды Лэмба, распространяющиеся в пьезопластинах ниобата лития (LiNbO3), танталата лития (LiTaO3) могут иметь коэффициент электромеханической связи К2 до 36%, а в ниобате калия (KNbO3) К2 до 100%. Кроме этого, в работе [4] показано, что SH0 мода Лэмба, распространяющаяся в пьезопластине 360-УХ-LiTaO3 при закорачивании обеих поверхностей становится термостабильной. Целью данной работы заключалась в численной оценке основных характеристик мод Лэмба, распространяющихся в пьезкристаллических пластинах при наличии на ее поверхности закорачивающих металлических пленок различного типа конечной толщины.
1. Методика численного эксперимента
Анализ характеристик волн Лэмба, распространяющихся в тонкой пьезоэлектрической пластине любого класса кристаллографической симметрии и любой ориентации, может быть осуществлен только численным способом, используя методику Фарнелла -Джонса [5]. Общее решение для механических смещений ui и электрического потенциала j можно представить в виде суммы 8-ми парциальных волн:
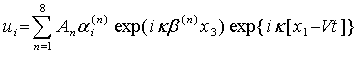 (1)
(1) 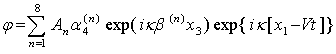
Здесь αi(n) (i = 1, 2, 3), An - амплитудные коэффициенты, β(n) - коэффициенты затухания вдоль оси Х3, к - волновое число, V- скорость, t - время.
Подставив общее решение (1) в связанные уравнения теории упругости для пьезосреды [5] и воспользовавшись граничными условиями [3], можно вычислить фазовую скорость V мод Лэмба. В случае, если на верхнюю (нижнюю) либо на обе поверхности пьезопластины толщины H нанесен металлический слой конечной толщины Нм, необходимо соответственно решать уравнения теории упругости как в самой пьезопластине, так и в материале металлической пленки. При этом соответственно усложнятся граничные условия [3]. После вычисления фазовой скорости V определенной моды можно определить коэффициент электромеханической связи (К2) для каждой моды. Величина К2 рассчитывается в соответствии с выражением [5]:
К2 = 2(V0 -VS)/V0, (2)
где V0 и VS - фазовые скорости волны на открытой и металлизированной поверхностях кристалла. В полубесконечном кристалле эта величина является однозначной для данной ориентации. По этой же формуле можно рассчитать величину К2 и для нормальных волн. При этом, в отличие от ПАВ, величина К2 для различных мод имеет пространственную дисперсию (зависит от относительной толщины пьезопластины Н/l). Заметим, что фазовая скорость волн Лэмба в пьезопластине зависит также от электрических граничных условий на нижней границе пластины (открытая или закороченная поверхность). Поэтому при вычислении величины К2 по относительной разности скоростей вдоль открытой и закороченной поверхности следует учитывать электрические граничные условия на нижней поверхности, которая может быть как открытой, так и закороченной. Если нижняя поверхность электрически закорочена, то скорости мод будут отличаться от соответствующих скоростей при открытой нижней поверхности. Рассчитанная в соответствии с (2) величина К2 также будет в этом случае другой. Наконец, в формулу (2) в качестве V0 можно подставить скорость V0, соответствующую обеим открытым поверхностям, а в качестве VS - скорость, соответствующую обеим закороченным поверхностям. Таким образом, можно получить три величины коэффициента электромеханической связи Ki2, i=1-3, соответствующие трем различным способам закорачивания электрического поля на границах пьезо-пластины.
2. Результаты и обсуждение
На рис. 1 представлены три варианта рассчитанных зависимостей Кi2 от H/λ (λ-длина волны) для нулевой антисимметричной моды Лэмба, распространяющейся в LiNbO3 YZ-среза. Как видно из рис.1 зависимость величины К2 от H/λ носит сложный характер, имеет максимумы при определенной величине H/λ (см. кривые 1-3). Фазовые скорости обеих нулевых мод (см. рис.1, кривая 4) при увеличении толщины пьезопластины H>3λ приближаются к скорости ПАВ в полубесконечной среде (VПАВ=3.487км/с). Величина К2 стремится к соответствующему значению для ПАВ (К2 ≈ 4.38%) не во всех случаях, что видно из рис.1. Если нижняя поверхность открыта, то величина К2 низкоскоростной моды (см. рис.1, кривая 1) стремится к соответствующей величине для ПАВ. Если нижняя поверхность закорочена, то наоборот (см. рис. 1. кривая 2). Если рассчитывать величину К2 в соответствии с (4) по скоростям, полученным при условии, что обе поверхности либо свободны, либо закорочены, то при увеличении толщины пластины К2 стремится к значению, соответствующему ПАВ (см. рис. 1, кривая 3). Кроме того, в этом случае получается самое большое значение К2 (около 11% для низкоскоростной моды вблизи H/λ = 0.55 (см. рис. 1, кривая 3).
Кривые на рис. 1 показывают также, что при любой толщине пластины для обеих нулевых мод выполняется условие K32 = K12 + K22, где нижние индексы соответствуют нумерации кривых на рис. 1.. На рис.2 показаны рассчитанный коэффициент электромеханической связи Кi2, (i=1,2,3) для низкоскоростной моды Лэмба в 420 УХ-LiTaO3 в зависимости от относительной толщины пластины Н/λ для случая, когда нижняя поверхность пластины открыта (К12, кривая 1K), нижняя поверхность закорочена (K22, кривая 2K) и обе поверхности закорочены (K32 , кривая 3K) и фазовой скорости V, когда обе поверхности пластины открыты (кривая 1V), одна поверхность закорочена (кривая 2V) и обе поверхности закорочены (кривая 3V).
Обычно срез и направление кристалле описывается тремя углами Эйлера (φ, θ, ψ) [5]. Первые два угла описывают срез кристалла, а третий угол- направление распространения волны.
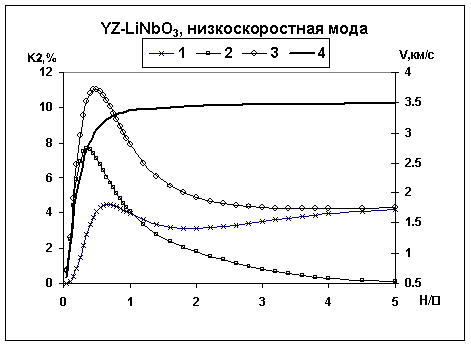
Рис. 1. Зависимости величины Кi2 и V от H/λ для низкоскоростной моды Лэмба в пьезопластине YZ-LiNbO3.
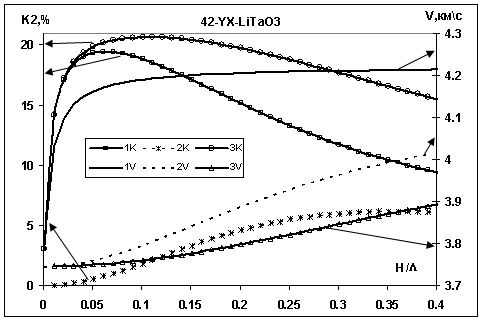
Рис. 2. Зависимость V (кривая 1V- обе стороны открыты, кривая 2V- одна сторона закорочена, 3V- обе стороны закорочены) и К2 (одна сторона пластины открыта (К12, кривая 1К), одна сторона закорочена (K22, кривая 2К) и обе стороны закорочены (K32 , кривая 3К) от H/λ.
На рис. 3 показаны рассчитанный температурный коэффициент задержки (ТКЗ) для низкоскоростной моды Лэмба в зависимости от 2-го угла Эйлера θ при относительной толщине пьезопластины LiTaO3 H/λ=0.1.
Из рис. 3 видно, что в интервале углов -650 < θ < 350 температурный коэффициент задержки (ТКЗ) для низкоскоростной моды Лэмба имеет 2 нулевых значения в случае, когда обе поверхности закорочены (кривая 3) и приближается к нулю при θ=-540, когда одна сторона закорочена (кривая 2). На рис.4 показана рассчитанная зависимость температурного коэффициента задержки (ТКЗ) низкоскоростной моды Лэмба от относительной толщины пьезопластины H/λ для 42-YX-LiTaO3 (углы Эйлера - (00 ,-480 ,00)).
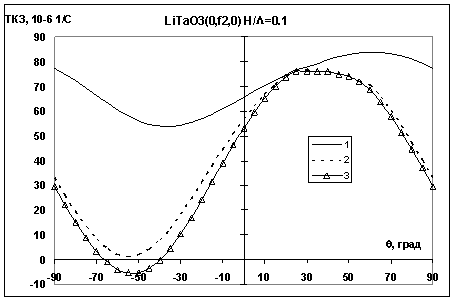
Рис. 3. Зависимость ТКЗ от θ (кривая 1- обе стороны открыты, кривая 2- одна сторона закорочена, кривая 3- обе стороны закорочены).
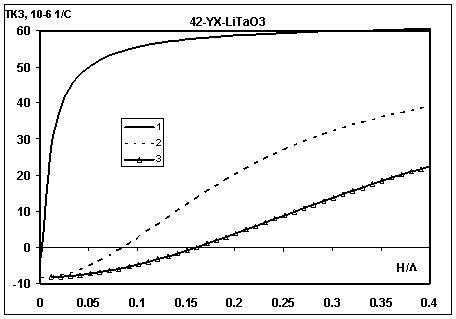
Рис. 4. Зависимость ТКЗ от H/λ (1 - обе стороны открыты, 2 - одна сторона закорочена, 3 - обе стороны закорочены).
Из рис. 4 видно, что для 42-YX-LiTaO3 ТКЗ~0 в случае, когда одна сторона пьезопластины закорочена (кривая 2) при H/l~0.16, когда обе стороны закорочены (кривая 3) при H/λ~0.17. Расчет для 36-YX-LiTaO3 (углы Эйлера - (00 ,-540 ,00)) показал ТКЗ~0 в случае, когда одна сторона пьезопластины закорочена при H/λ~0.1, когда обе стороны закорочены при H/λ~0.08.
В работе были рассчитаны характеристики низкоскоростной моды Лэмба при наличии на одной поверхности пьезопластины металлической пленки конечной толщины HМ . На рис. 5 показаны рассчитанные коэффициенты электромеханической связи К2 в зависимости от относительной толщины металлического слоя НМ/Δ для материалов Al, Cu, Au, Ni при относительной толщине Н/Δ=0.3 пьезопластины 420 УХ-LiTaO3. Из рис. 5 видно, что величина К2 увеличивается и может достигать очень высоких значений при определенных толщинах металлической пленки. Например, для Au - К2=80% при Hм/λ=0.2, для Cu - К2=71% при Hм/λ=0.3, для Ni - К2=70% при Hм/λ=0.3, для Al - К2=31% при Hм/λ=0.4. Материальные константы для LiNbO3, LiTaO3 и для металлов были взяты из работ [6,7].
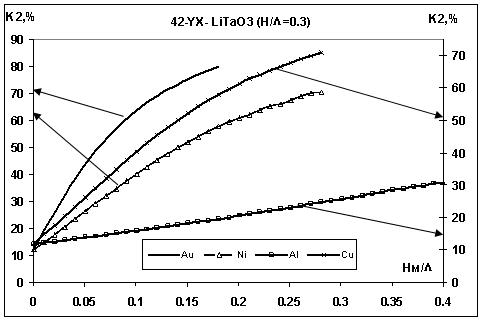
Рис. 5. Зависимость К2 от Hм /λ для пленок Al, Au, Cu, Ni. Н/Δ=0.3
Заключение
Таким образом, в работе теоретически рассчитаны характеристики мод Лэмба, распространяющихся в системе «пьезопластина - металлический слой конечной толщины». Показано, что используя различные типы металлического слоя конечной толщины можно существенно увеличить величину коэффициента электромеханической связи для мод Лэмба. Например, для пьезопластины 420 УХ-LiTaO3 (относительная толщина Н/Δ=0.3) при наличии пленки Au (относительная толщина Hм/λ=0.2) - К2=80% , для пленки Cu - К2=71% при Hм/λ=0.3, для пленки Ni - К2=70% при Hм/λ=0.3, для пленки Al - К2=31% при Hм/λ=0.4.
СПИСОК ЛИТЕРАТУРЫ:
- Adler Е. Electromechanical coupling to Lamb and Shear-Horizontal modes in piezoelectric plates // Proc. IEEE Trans. on Ultrason., Ferroelectr. and Freq. Contr. -1989. - V. 36. - No.2. - P. 223-230.
- Джоши С.Г., Зайцев Б.Д., Кузнецова И.Е. SH акустические волны в пластине ниобата лития и влияние электрических условий на их свойства // Акустический журнал. - 2001. - Т.47. -№3. - С. 336-340.
- Двоешерстов М.Ю., Петров С.Г., Чередник В.И., Чириманов А.П. Электроакустические волны Лэмба в пьезокристаллических пластинах // Акустический журнал. - 2004. - Том 50. - №5. - С.633-639.
- Fujiwara H., Yamazaki D., Nakamura K. Temperature characteristics of SH-type acoustic waves in rotated Y-cut LiTaO3 thin plate // IEEE Ultrason. Symp. - 2005.- P. 1864-1867.
- Мэттьюз Г. Фильтры на поверхностных акустических волнах. М.: Радио и связь.- 1981. - 470 C.
- Covacs G., Anhorn M., Engan H., Visintini G. and etc. Improved Material Constants for LiNbO3 and LiTaO3 // Proc. IEEE Ultrason. Symp. - 1990. - P.435.
- Ballandras S., Gavignet E., Bigler E., Henry H.. Elastic constants, temperature constants and thermal expansion coefficient // Appl. Phys. Letters.- Vol. 71.- No 12.- 1997.- Р. 1625-1627.



