Анализируя это выражение можно вывести общую зависимость числа выполняемых при вычислении элементарных математических операций от количества членов аппроксимирующего ряда. Для n≥1 получим:
,
Данные выражения, могут быть использованы как для оценки необходимых для реализации аппаратных ресурсов ПЛИС, так и при известности времени выполнения элементарных математических операций и условии, что все операции выполняются строго последовательно, для определения суммарного времени вычисления значения функции.
Расчеты показывают, что при 
например, для получения относительной ошибки вычисления 
необходимо использовать 7 членов ряда 
. При реализации на ПЛИС это потребует использования 7 сумматоров и 12 умножителей.
Из математики известно, что для получения многочлена, наименее отклоняющегося от заданной функции необходимо использовать его разложение по многочленам Чебышева. Для исследуемой функции это разложение имеет вид:
,
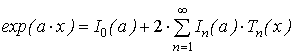где: 
и 
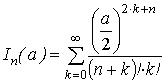- функции Бесселя мнимого аргумента порядка n;Tn(x) - многочлены Чебышева от аргумента функции.
Как следует из приведенных выражений, величины I0 (a) и In(a) при известном значении являются константами и могут быть вычислены заблаговременно.
Ниже в таблице 1 приведено соотношение между числом членов суммы разложения по многочленам Чебышева, относительной погрешностью вычисления и числом выполняемых операций.
Таблица 1
|
Число членов ряда |
1 |
2 |
3 |
4 |
5 |
|
Относительная погрешность |
2.83 % |
0.54 % |
0.0256 % |
4.47e-3 % |
2.52e-4 % |
|
Количество операций |
NSUM =1 NMULT = 1 |
NSUM =3 NSUM =3 |
NSUM =5 NSUM =6 |
NSUM =8 NSUM =8 |
NSUM =11 NSUM =12 |
В этом случае при |x|≤1 для получения относительной ошибки вычисления необходимо использовать 5 членов ряда 
. Однако число выполняемых при этом операций увеличивается.
Известны методы повышения точности вычисления функции, основанные на масштабировании ее аргументы. Проведем в исходном разложении замену:
.
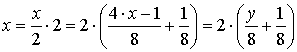В этом случае расчетное выражение для функции примет вид:
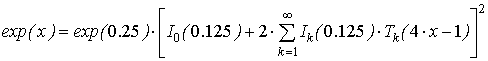
Теперь для получения относительной ошибки вычисления в том же диапазоне изменения аргумента на уровне достаточно использование только двух членов ряда 
и вычисление функции потребует выполнения 6 операций сложения и 5 операций умножения.
Последний алгоритм был положен в основу разработки вычислителя функции exp(x) с использованием ПЛИС фирмы Altera.
В таблице 2 приведены результаты исследования модели разработанного устройства
Таблица 2.
|
Значение аргумента |
0.109375 |
0.3046875 |
0.5 |
0.625 |
0.90625 |
|
Относительная ошибка |
1.452664e-4 |
1.472459e-4 |
4.115197e-4 |
6.841889e-3 |
0.075145 |
При вычислении функций Бесселя учитывалось, как минимум, 7 правильных десятичных знаков после запятой, что соответствует 24 разрядам дробной части двоичного числа 
. Разрядность аргумента функции - 8 бит дробной части. 
На основании изложенного можно сделать вывод, что применение при вычислении функции exp(x) разложения по многочленам Чебышева позволяет, как уменьшить необходимые для реализации аппаратные ресурсы ПЛИС, так и уменьшить суммарное время ее вычисления.