
Для молекул 4-алкил-1,3,2-диоксаборинанов, благодаря снижению числа несвязанных взаимодействий из-за плоской конфигурации тригонального атома бора, можно ожидать более высокого - по сравнению с однотипно замещенными 1,3-диоксанами - содержания альтернативного конформера. Это должно отразиться на параметрах конформационного равновесия (значения свободной конформационной энергии заместителя у атома С4 ∆G0 и расчетной высоты активационного барьера ∆E≠). Данные настоящей работы показывают, что для циклических эфиров 1-3 характерна равновесная форма Се.
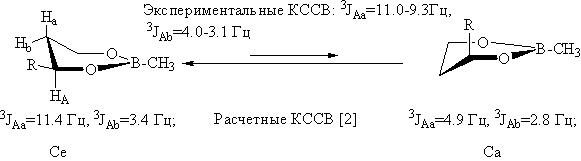
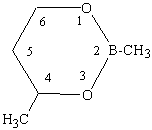
На примере эфира 1 показано (ММ+), что наиболее оптимальный маршрут инверсии кольца связан с изменением (сканированием) торсионного угла 1-6-5-4 (табл.1). Сканирование углов 1-2-3-4 и 3-4-6-1 к инверсии не ведет.
Таблица 1. Барьеры инверсии (ккал/моль) конформеров Се↔Са эфира (1)
|
Угол |
2-3-4-5 |
3-4-5-6 |
1-6-5-4 |
2-1-6-5 |
2-3-5-6 |
|
∆Е≠ |
8.2 |
7.4 |
7.0 |
7.4 |
8.6 |
|
ПС |
2,5-Т |
2,5-Т |
2,5-Т |
2,5-Т |
2,5-Т |
|
Угол |
2-1-5-4 |
2-1-6-4 |
2-3-4-6 |
1-2-3-5 |
4-5-6-2 |
|
∆Е≠ |
9.1 |
18.6 |
17.0 |
36.4 |
9.8 |
|
ПС |
2,5-Т |
2,5-Т |
2,5-Т |
С* |
2,5-Т |
* Конформация софы с планарным фрагментом 3-4-5-6.
Оптимальный маршрут инверсии включает переходное состояние (ПС), отвечающее форме 2,5-Т.

Величина ∆Е≠ эфира 1, рассчитанная различными методами (табл.2), несколько меньше, чем у 2,5-диметиланалога [8]; это, наряду со снижением ∆G0 группы С4-СН3 по сравнению с аналогичной величиной в 1,3-диоксанах [9], свидетельствует о более высокой конформационной гибкости молекул соединения 1.
Расчет ∆Е≠ выполнен с помощью методов АМ1 и ab initio в рамках алгоритмов собственных значений (СЗ) и реакционных карт (РК) [7], при этом данные АМ1 отличаются более низким барьером активации (табл.2). Следует отметить, что для молекул шестичленных циклических борных эфиров характерны достаточно невысокие - по сравнению с однотипно замещенными 1,3-диоксанами - значения барьеров активации, составляющие в случае алкилзамещенных аналогов 7-8 ккал/моль [5].
Важной характеристикой формы цикла являются параметры складчатости Зефирова-Палюлина-Дашевской [10]. Их расчет для ПС эфира 1 с использованием геометрических данных метода 3-21G показал, что полученные значения (s=0.63, Θ=91.00, Ψ=28.50), близки к характеристикам классической твист-формы (Θ=900, Ψ=300) [10].
Таблица 2. Параметры конформационного равновесия (ккал/моль) циклических эфиров 1-3
|
№ |
Метод расчета |
∆Е
|
∆Е≠
|
∆G0
|
Эксперимент. ∆G0 в 1,3-диоксанах |
|
1
2
3 |
ММ+ АМ1 STO-3G 3-21G MM+ AM1 MM+ AM1 |
0.8 0.3 0.9 0.6 1.2 0.2 1.2 0.2 |
7.0 3.5 6.8 8.1 7.1 - 7.1 - |
0.7
1.4 1.4 1.4 1.4 |
2.72-2.92 [9]
-
- |
Для расчета значений ∆Е≠ молекул эфиров 2 и 3 методом ММ+ в качестве реакционной координаты, определяющей маршрут инверсии, использован торсионный угол 1-6-5-4. Конформационный объем заместителей в этих соединениях заметно превышает размеры метильной группы, что приводит к определенному увеличению величины ∆G0 для эфиров 2 и 3. Однако существенных различий в значениях ∆Е≠ соединений 1-3 не наблюдается; это также свидетельствует о повышенной конформационной гибкости молекул 4-алкил-1,3,2-диоксаборинанов.
СПИСОК ЛИТЕРАТУРЫ
- Грень А.И., Кузнецов В.В. Химия циклических эфиров борных кислот. Киев: Наукова думка, 1988. - 160 с.
- Кузнецов В.В. Автореф. дисс. докт. хим. наук. Уфа, 2002. - 47 с.
- Rossi K., Pihlaya K. //Acta Chem. Scand. - 1985. - V.B 39, N 8. - P.671.
- Валиахметова О.Ю., Бочкор С.А., Кузнецов В.В. //Баш. хим. журн. - 2004. - Т. 11, №1 . - С.79.
- Кузнецов В.В., Новиков А.Н. //Химия гетероцикл. соединений. - 2003. - №2. - С.295.
- Валиахметова О.Ю., Бочкор С.А., Кузнецов В.В. //Фундаментальные исследования. - 2005. - № 3. - С.38.
- HyperChem 7.01. Trial version. http://www.hyper.com/.
- Кузнецов В.В., Новиков А.Н. Рублев И.С. Марколенко П.Ю. //Химия гетероцикл. соединений. - 2003. - №3. - 426.
- Гиттинс В.М., Уин-Джонс Е., Уайт Р.Ф. //в кн. Внутреннее вращение молекул / под ред. В.Дж. Орвилл-Томаса. - М.: Мир, 1977. - С.352.
- Zefirov N.S., Palyulin V.A., Dashevskaya E.E. //J. Phys. Org. Chem. - 1990. - V.3, №3. - P.147.



