На примере стационарной электродинамической задачи возбуждения однородной сферы проводится сравнение двух модификаций метода вспомогательных источников. В обычном методе вспомогательных источников численное решение задач наталкивается на значительные трудности из-за того, что внутреннее поле представлено полями внешних источников, что в некоторых случаях приводит к неестественно большой размерности аппроксимации внутреннего поля. При этом вспомогательные источники для представления искомого решения выбираются так, чтобы элементарные токи и заряды были локализованы на фиктивных вспомогательных поверхностях, обычно конформных действительной поверхности границы раздела [1-2-3-4]. В предлагаемой в настоящей работе новой модификации метода внутреннее поле представлено в виде суммы стоячих сферических волн, центры которых одновременно совпадают с точками размещения вспомогательных источников, представляющих внешнее поле. Это позволило в два раза снизить размерность задачи при сохранении точности решения.
1- Теоретическая формулировка.
Рассматривается однородная сфера, для которой в предлагаемой модификации метода вспомогательных источников поле рассеяния вне сферы рассматривается как исходящее от набора вспомогательных источников, расположенных внутри сферы, а поле, проникающее внутрь сферы, представлено в виде совокупности стоячих сферических волн с центрами в тех же точках, где размещены вспомогательные источники внешнего поля. Поля, внутри и вне сферы, находятся из условия непрерывности тангенциальных составляющих поля на дискретном множестве точек на поверхности сферы. В результате получается набор матричных уравнений, из которых должны быть определены амплитуды вспомогательных источников и амплитуды сферических волн. Как только амплитуды найдены, решение завершено: магнитные и электрические поля и их параметры легко вычисляются с помощью найденных представлений внутренних и внешних полей [5-6].
Практически в представленном методе нам нужны только точки на поверхности раздела (на сфере), количество и расположение вспомогательных источников. При этом нет необходимости в детальном объемном или поверхностном описании структуры, как требуется другими методами (метод конечных элементов, метод граничных элементов и т.д.) [7].
Внешнее поле рассеяния, излучающееся в окружающее пространство, описывается в виде суммы полей внутренних вспомогательных источников:
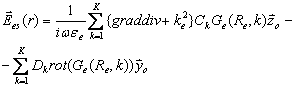(1)
(2)
где 
-скалярная функция Грина однородного пространства
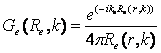(3)
Внутреннее поле представляется в виде совокупности сферических стоячих волн:
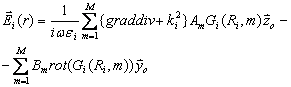(4)
(5)
где вместо функции Грина используется функция
(6)
Присутствие такой функции поля в этой формуле означает, что вспомогательные поля представляют собой стоячие сферические волны, центры которых, играющие роль точек размещения вспомогательных источников, могут быть расположены внутри сферы. Падающее электромагнитное поле, излучаемое дипольной антенной, вычисляется по формулам:
(7)
, (8)
а полное поле соответственно в виде суммы:
(10)
, (11)
где 
, 
- падающее поле, 
, 
- поле рассеяния и 
, 
- полное поле. 
, 
- поле внутри сферы. Решение метода вспомогательных источников (МВИ) получается из условия непрерывности тангенциальных составляющих поля на поверхности сферы S. С помощью этих граничных условий в точках N на поверхности сферы S получены уравнения (3-12) и (3-13). Как и прежде, из решения уравнений граничных условий (3-12) и (3-13) определяются неизвестные вспомогательные источники, и могут быть вычислены электрическое и магнитное внутреннее поле и электрическое и магнитное поля рассеяния в любой точке.
,(12)
,(13)
где: 
- единичный вектор, нормальный к поверхности S в любой точке.
Из решения матричных уравнений (3-12) и (3-13), определяются неизвестные Am, Bm, Ck and Dk, и внутренние и рассеивающиеся поля могут быть определены в любой точке [8].
2- Результаты и выводы.
Следующие результаты представляют собой сравнение между примененным методом вспомогательных источников и обычным методом вспомогательных источников. Все результаты получены при 900 МГц, и сфера имеет электрические параметры εr = 45.8, σ = 0.77 Сим/м. Максимальные погрешности составляют около 1.69% и 1.99% для двух методов соответственно. Рассчитано отношение рассеиваемых электрических полей в обоих методах к расстоянию от поверхности сферы для расстояний от поверхности сферы от (λo/12) до (5λo), при θ =π/4, и 
, а также отношение рассеиваемых электрических полей в обоих методах к сферическому полярному углу (θ) на расстоянии от поверхности сферы λo, и . Рассчитаны внутренние электрические поля вдоль оси X. Ось X пересекает ось сферы и точку размещения диполя, находящуюся в направлении оси z и в точке x=115мм, где расстояние между диполем и поверхностью сферы 15мм.
Заключение
Отмечается хорошее согласие между результатами нового метода вспомогательных источников и результатов обычного метода вспомогательных источников, при том, что новый более прост и позволяет легко найти положение вспомогательных источников. Число неизвестных при применении нового метода составило 9 против 16 в обычном методе соответственно при максимальных погрешностях 1.69 % и 1.99 %.
СПИСОК ЛИТЕРАТУРЫ
- J.C.Monzon: Scattering by a Biisotropic Body. IEEE Trans. Antennas Prop. 43 (1995) 11, 1273-1282.
- Dautov O.S., Adel Zein E.M. Method of auxiliary sources for calculating the SAR through the sphere modeling human head //Environmental radioecology and applied ecology. - Vol. 10 No. 3, 2004 - p.p. 9-16.
- Claude, M.V., "Absorption Characteristics of Multilayered Sphere Models Exposed to UHF/Microwave Radiation", IEEE Transactions on Biomedical Engineering, Vol.22, No.6, 1994.
- Shubitidze, F., H. Anastassiu, and D. Kaklamani, "An improved accuracy version of the method of auxiliary sources for computational electromagnetics", IEEE Trans. Antennas Propagation, 2002.
- Shubitidze, F., K. O´Neill, S. A. Haider, K. Sun, and K. D. Paulsen, "Application of the method of auxiliary sources to the wideband electromagnetic induction problem", IEEE Trans. Geosci. Remote Sensing, 40, 928, 2002b.
- Anastassiu, H.T., D. I. Kaklamani, D. P. Economou, and O. Breinbjerg, "Electromagnetic scattering analysis of coated conductors with edges using the method of auxiliary sources in conjunction with the standard impedance boundary condition (sibc)", IEEE Trans. Antennas Propagation, 50, 59, 2002.
- S. G. Shepherd and F. Shubitidze, Thayer School of Engineering, Dartmouth College, Hanover, New Hampshire, "Method of auxiliary sources for calculating the magnetic and electric fields induced in a layered Earth" USA November 13, 2002.
- Bogdanov F.G., Karkashadze D.D., Jobava R.G., Zaridze R.S.: Method of auxiliary sources for diffraction problems in complex media. Abstracts of International Symposium (PIERS), Cambridge, Massachusetts, USA (1997), 863.