(I.1)
, (I.2)
. (I.3)
In this problem constant 
and the functions 
are determined as follows:
;
where 
and 
are constants 
and 
is function
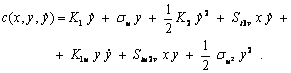
In the case 
the problem (I.1) - (I.3) may be a problem with a point of singularity. The solution of this problem will simplify to a singularity point and can be determined by a generalized power series[1].
II. The inverse problem for calculus of variations [3] for the problem (I.1) - (I.3) is searching a functional with Lagrangian 
, where the following are defined:
.
The equation (I.1) must be the Euler - Lagrange equation as follows
.
One from solutions of this problem is [1]:
(II.1)
In last formula constants before argument t , variables 
are defined from statement of a problem.
III. Applications. The formulas (I.1) - (I.3), (II.1) have next applications: curves with a point of return (a brachistochrone, Nail parabola), a dynamics problem with variable mass (the management of a movement of the rubbish collector in the space around the earth), the problem of finding an optimal shape of a body in hypersonic flow near a point of singularity [1].
References
- Svyatskov V.A. 2000. The equation of Euler - Lagrange in boundary layer with applications. Cheboksary, Chuvash State Pedagogical University, 165 p. (in Russian).
- Svyatskov V.A. One Metod of Calculation for Optimal Shape of a Body in Hypersonic Flow near a Singular Point.//High Speed Hydrodynamics. The Intetnational Summer Scientific School. - Russia, Cheboksary: 2002. - pp. 383 - 388.
- Bronshtein I.N. and Semendyaev K.A. The Handbook on Mathematics for Engineers and Students. - M.: Nauka. - 1986. - 544 p. (in Russian).