Одним из наиболее мощных прикладных методов цифровой обработки сигналов является вейвлет-анализ. В его основе лежит вейвлет-преобразование, базисные функции которого, в отличие от базисных функций преобразования Фурье, обладают как пространственной, так и временной локализацией. Эта особенность позволяет использовать вейвлет-преобразование при анализе нестационарных сигналов, содержащих ограниченные по времени компоненты.
Существует непрерывное и дискретное вейвлет-преобразование. Непрерывное вейвлет - преобразование требует больших вычислительных затрат и поэтому не может быть использовано в современных системах управления реального времени. Дискретное вейвлет-преобразование определяется формулами:

Наборы коэффициентов c и d называются, соответственно, аппроксимирующими и детализирующими коэффициентами. Фильтры h и g называются вейвлет-фильтрами и строятся на основе вейвлет-функций. Аппроксимирующие коэффициенты соответствуют низкочастотной части сигнала, детализирующие коэффициенты - высокочастотной. В большинстве реальных сигналов информация содержится в области низких частот, а в области высоких частот сосредоточены помехи и случайные возмущения. Следовательно, дискретное преобразование может быть применено как для отделения полезного сигнала от шума, так и для выделения кратковременных высокочастотных возмущений.
Системы управления реального времени должны обрабатывать большие объемы информации и делать это достаточно быстро. Высокие требования могут предъявляться и к точности вычислений. Повышение скорости и точности вычислений может быть достигнуто в результате перехода к целочисленной арифметике. Обычно обрабатываемый сигнал получается с выхода аналогово-цифрового преобразователя, а, значит, состоят из целых величин. Однако коэффициенты вейвлет-фильтров, как правило, представляют собой действительные числа. Задача перехода к целочисленной арифметике сводится к построению целочисленных вейвлет-фильтров.
В работе [2] для построения целочисленного преобразования используется лифтинг - техника построения вейвлетов с заданными свойствами. Один из полученных вариантов преобразования определяется формулами:
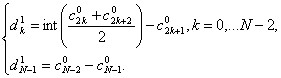
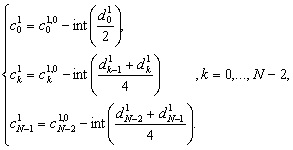
Для сравнения эффективности оба метода были реализованы на программируемом логическом контроллере S7-226 фирмы Siemens. Для реализации использован язык Layer Diagram (LAD), входящий в семейство индустриальных языков программирования, определяемых стандартом МЭК 1131-3. Для дискретного вейвлет-преобразования число операций действительного сложения и умножения определяется формулами (n - длина сигнала, L - длина вейвлет-фильтра):
![]() (1)
(1)
При реализации целочисленного вейвлет-преобразования требуется n операций целочисленного умножения и 14n+5 операций сложения.
Операция целочисленного сложения требует 29 мкс, целочисленного умножения - 47 мкс, действительного сложения - 71 мкс, действительного умножения - 55 мкс. Пусть требуется обработка сигнала, содержащего 1000 отсчетов. При дискретном преобразовании используется вейвлет-фильтр Добеши 6-го порядка, содержащий 12 коэффициентов. Тогда, в случае обработки сигнала единым блоком, дискретное преобразование потребует приблизительно 2,5 с, в то время как дискретное - только 0,447 с.
Таким образом, несмотря на сложность построения целочисленного вейвлет преобразования, его использование позволяет достичь большей скорости обработки сигналов, что является очень важным при реализации систем управления реального времени.
СПИСОК ЛИТЕРАТУРЫ
- S7-200 Programmable Controller System Manual. Siemens AG, 2004.
- Воробьев В.И., Грибунин В.Г. Теория и практика вейвлет-преобразования. СПб.: Изд-во ВУС, 1999.
- Добеши И. Десять лекций по вейвлетам. Москва-Ижевск: НИЦ «Регулярная и хаотическая динамика», 2004.
- Каримов Р.Н. Основы теории случайных процессов. Волгоград: РПК «Политехник», 2003.



