1. Рассмотрим прямоугольную решетку [1], составленную из N=N1N2 упругих линейных струн, защемленных на концах. Конструкция образована системой прямоугольных ячеек (длины- Δl1,2; вершины - точечные абсолютно твердые тела с массами m). Возбуждение осуществляют случайные широкополосные силы (типа белых шумов). Каждая струна (длины l1,2, натяжения -T1,2) нумеруется индексами k=1,2,., N1 и q= 1,2.. N2. Динамика решетчатой конструкции описывается посредством N функций прогибов ukq(t). Каждая из функций ukq(t) изменяется вдоль некоторой оси, перпендикулярной плоскости статического равновесия решетки (рис. 1).
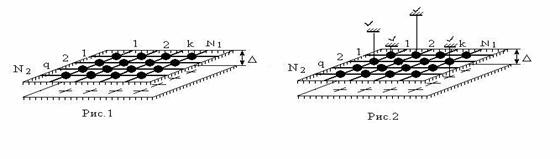
Параллельно плоскости статического равновесия решетки на расстояниях Δkq>0 и Δ 2kq<0 от каждого из узлов установлены ограничители хода, с которыми точечные тела, находящиеся в узлах решетки могут совершать абсолютно упругие соударения; удары предполагаются прямыми и центральными. Ограничители могут располагаться произвольно. На рис. 1 показан случай одностороннего ограничителя, представляющего собой прямую стенку. На рис.2 с противоположенной стороны показано несколько прямых ограничителей - помечены штриховкой и «галочками».
Таким образом, если при t=t0 и (или) при t=t0 для каких либо k и q происходит соударение с верхним или нижним ограничителями, то [1]
ukq(t0-0)=-ukq(t)(t0+0)<0, ukq(t0)=Δ1kq>0; ukq(t0-0)=-ukq(t)(t0+0)>0, ukq(t)=Δ2kq<0; Δkq ≤ukq(t)≤ Δ2kq. (1)
Пусть вынуждающие силы, действующие на узлы [1], даются случайными некоррелированными широкополосными процессами ξ kq(t) типа белых шумов. Пусть < ξ kq ξ rs >=2S δ kq δ rs δ (t - t/); δ kq, δ rs -символы Кронекера (k, q =1,2,.. N1; r, s=1,2,.. N2); δt - δ-функция Дирака. Считая, что координаты ukq(t) отсчитываются от точек, лежащих в плоскости равновесия конструкции, а, также предполагая, что рассеяние энергии пропорционально абсолютным скоростям каждого узла, запишем систему уравнений, описывающую движение решетчатой конструкции в промежутках между соударениями. Так как каждая частица лежит одновременно на двух струнах, то получим N уравнений:
mukq+bukq+c1(2ukq-u(k-1,q)-u(k+1,q))+c2(2ukq-u(k,q-1)-u(k,q+1)) = ξ kq(t); (2)
здесь соответственно обозначено: с1,2 =T1,2 Δl1,2- коэффициенты упругости b - коэффициент демпфирования. Граничные условия ukq=0, при k=0;(N1+1) и q=0;(N2+1) [1].Определяющая уравнения движения функция Гамильтона системы (2) H(ukq;ykq)
Н(ukq; ykq)=Σ½y2kq+½[Σ с1(uk1 - uk,N2)2+ Σ c2(u1q -uN1,q)2+
(k, q) (k) (q)
+ Σ с2(ukq-uk,(q-1))2+ Σ c1(u1q-uN1,q)2]+......., (3)
(k=2) (q=2)
где введено обозначение ykq 
ukqt. Без ограничения общности положим m=1, так что гамильтоновы переменные - (ykq,ukq).
2. Для описания процесса воспользуемся методами ДМП [1]. Предполагая процесс стационарным, будем искать 2N - мерную стационарную плотность вероятностей p(ukq,ykq); и запишем уравнение ФПК для уравнений (1) [1]:
Σ[{Н,p}kq - b δ/ δ ykq(ykqp) ½S δ2p/ δy2kq] = 0, (4)
(k, q)
{Н,p}kq)(δH / ykq)(δukq)- (δH / δukq)(δp /ykq) - скобка Пуассона для узла решетки. Уравнение (4) необходимо решать с учетом условий (1). Функция p(ukq(t);ykq(t)) от 2N (N=N1N2) переменных, удовлетворяющая (4) и сформулированным ограничениям, описывает известное распределение Гиббса [1], имеющее вид: p(ukq;ykq)=Cexp{-(2b/S)[H(ukq;ykq)]}, ukq€X={ukq|Δ1kq ≤ukq(t) ≤ Δ 2kq}, С - постоянная нормировки. Распределение (4) удовлетворяет всем данным выше условиям. При его посредстве можно полностью и в рамках данной модели точно описать искомый процесс.
СПИСОК ЛИТЕРАТУРЫ:
- Крупенин В.Л. Случайные соударения решетчатой конструкции с периодической структурой и плоским ограничителем хода ДАН, 2006 - т.2-с. 1-4.