Рассмотрим поверхность контакта торсионного вала и ролика в виде тора по внешней поверхности цилиндра.
Уравнение поверхности тора, внедряемой в торсионный вал, в декартовой системе координат запишется:
![]()
Переходя к цилиндрической системе координат, найдем частные производные:
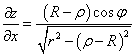 ,
, 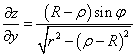 .
.
Далее находим элемент площади
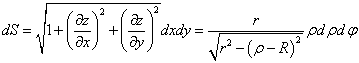 .
.
Вычисляем площадь поверхности в цилиндрической системе координат по формуле:
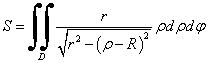 .
.
Область интегрирования D ограничена с одной стороны уравнением окружности сечения цилиндра, а с другой стороны уравнением внешней окружности тора ρ = R, тогда в полярной системе координат площадь поверхности пятна вычисляется по формуле:
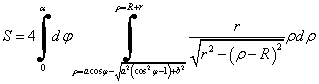 .
.
Для нахождения предельного угла интегрирования α найдем координаты точек пересечения окружности цилиндра и окружности тора.
Площадь пятна контакта определяется как сумма площадей контакта в зонах пластической и упругой деформации. Сначала найдем площадь пятна контакта в зоне пластической деформации при заданных значениях размеров вала и ролика (в мм ).
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() мм2
мм2
Затем найдем площадь пятна контакта в зоне упругой деформации при b = 29,55:
![]() мм2
мм2
Общая площадь пятна контакта: ![]() мм2
мм2



