В случае рассмотрения структурновязкой жидкости без предела текучести, после перехода к безразмерным параметрам рассматриваемая система уравнений выглядит следующим образом:
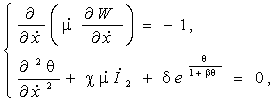(1)
где 
- безразмерная поперечная координата, 
- безразмерные скорость, вязкость и температура; α,β - безразмерные параметры, характеризующие энергию активации вязкого течения χ,δ безразмерной параметры, характеризующий интенсивность химического и диссипативного тепловыделения .
Граничные условия первого рода имеют вид: 
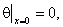
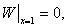
(2)
В качестве реологической модели, которая описывает зависимость текучести жидкости от температуры, используется модель Кутателадзе-Хабахпашевой [2] для структурно вязкой жидкости, а температурные зависимости параметров реологической модели представляются в аррениусовском виде.
Вначале были рассмотрены зависимости безразмерной температуры и вязкости в центре канала от параметров α энергии активации вязкого течения. Оказалось, что они имеют вид S-образных кривых, а при увеличении χ кривые сужаются. Как показали расчеты, интервал неоднозначности решений температуры, скорости и вязкости в зависимости от величины энергии активации вязкого течения при увеличении параметра χ уменьшается.
Зависимости безразмерной температуры и вязкости от параметров β - безразмерного параметра, обратно пропорционального энергии активации химической реакции также имеют вид S-образных кривых, но в отличии от α они направлены в обратную сторону. А при увеличении χ они также как и для α сжимаются.
Интервал неоднозначности решений температуры и вязкости в зависимости от величины при увеличении параметра также как и в зависимости от уменьшается.
ЛИТЕРАТУРА:
- Буевич Ю.А, Заславский М.И. О гидродинамическом тепловом взрыве в радиальном подшипнике // ИФЖ. 1982. Т. 142, № 5 C. 813819.
- Кутателадзе С.С., Попов В.И., Хабахпашева Е.М. К гидродинамике жидкостей с переменной вязкостью // ПМТФ. 1966. № 1. С.4549.