Для повышения качества ремонтно-восстановительных работ, уровня его экологической безопасности перспективно освоение и внедрение современных методов управления технологическими процессами (ТП) с использованием компьютерных технологий. Реализация такой задачи связана с исследованием и применением традиционных и новых эффективных методов и средств моделирования, построением универсальных и экономичных математических моделей (ММ). На их основе разрабатываются компьютерные программные комплексы, которые должны быть адаптированы к заданной производственной среде, легко встраиваться в общую систему управления ремонтным процессом и обеспечивать работу в режиме реального времени.
Следует отметить, что в практике отечественного ремонтного производства еще крайне редко применяется компьютерное моделирование. При внедрении новых и корректировке уже используемых технологий задача отработки ТП обычно решается чисто эмпирическим путем - методом проб и ошибок. Такой подход требует большого числа натурных опытов, что сопровождается значительными расходами временных, энергетических и материальных ресурсов.
На примере выбранной технологии, применяющейся в ремонтно-восстановительном производстве, нами разрабатывались универсальные алгоритмы, адекватные реальным условиям ММ и компьютерные программы, которые позволяют управлять качеством ТП автотранспортной и сельскохозяйственной техники.
Наиболее приемлемый способ решения подобных задач - это применение компьютерно-адаптированного эмпирического подхода. В этом случае алгоритм построения ММ не зависит от физической природы объекта, а сами эмпирические модели объективно отражают с определенной точностью поведение рассматриваемого ТП или отдельных операций в границах выделенного исследователем факторного пространства.
По результатам экспериментальных исследований формируются базы данных в форме электронных информационных таблиц, из которых в соответствии с задачами исследования можно выделить матрицу выходных сигналов (откликов) Y и матрицу входных параметров (факторов) Х.
Были исследованы следующие методы построения ММ: традиционный статистический (построение полиномиальной модели) и основанный на нейросетевом аппарате (построение искусственной нейронной сети (ИНС)). Рассмотрены возможности их применения для управления ТП ремонтного производства.
В первом случае результатом моделирования является аналитическое уравнение - полином некоторой степени:
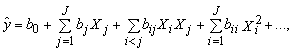(1)
где 
- рассчитанное по модели значение отклика технологического процесса; b0, bj - постоянные коэффициенты; Xij - значение J независимых (некоррелированных) факторов, i, j = 1,2,...,J.
Исследование полученных полиномов проводится с использованием классического аппарата регрессионного анализа [1].
Моделирование с помощью нейросетевого аппарата необходимо проводить по следующим этапам:
- выбрать подмножество элементов для ввода и вывода информации;
- выбрать архитектуру ИНС (топологию межнейронных связей);
- выбрать метод обучения ИНС.
Для построения эмпирических ММ сложных ТП удобно использовать многослойную ИНС, структура которой показана на рисунке 1 (многослойный персептрон). Такая ИНС состоит из нескольких слоев нейронов (общее число слоев - К, входной слой считается нулевым), которые получают, обрабатывают и передают информацию относительно связей входных параметров и соответствующих откликов.
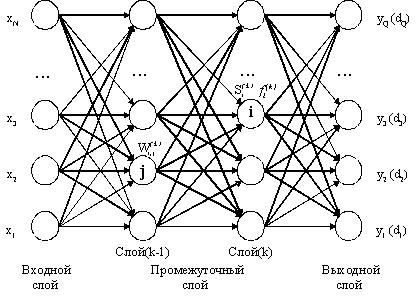
Рисунок 1. Структура многослойной нейронной сети
Во входном слое имеем N образов х, в выходном слое - Q образов у. В сеть входит промежуточный слой нейронов, которые не взаимодействуют с «внешней средой», а выполняют классификацию и экстракцию признаков по информации, обеспечиваемой входными и выходными слоями. На приведенном рисунке 
- весовой коэффициент синоптической связи, соединяющей j-ый нейрон слоя (k-1) с i-ым нейроном слоя k; 
- вход i-го нейрона в k-ом слое; 
- вычисленный выход i-го нейрона в k-ом слое; 
- требуемый выход i-го нейрона. Величина является взвешенной суммой входных сигналов нейрона:
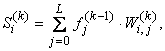(2)
где L - число нейронов в слое (k-1) с учетом нейрона с постоянным выходным состоянием +1, задающего смещение.
Выход данного нейрона - это функция активации. Целесообразно выбрать сигмоидальную функцию активации, которая наделяет ИНС способностью создавать модели с дополнительной степенью свободы (что недоступно в статистических регрессионных методах). Она определяется следующим образом:
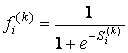. (3)
Для обучения ИНС использовался алгоритм обратного распространения ошибки [2,3].
Конкретным объектом моделирования был выбран один из самых перспективных ресурсосберегающих способов восстановления и (или) упрочнения изношенных деталей машин - микродуговое оксидирование (МДО). С его помощью можно наносить качественные покрытия, характеризующиеся высокой износостойкостью.
Натурные эксперименты осуществлялись на образцах из различных алюминиевых сплавов (АК9М2, АМг6, АК5) с использованием электролита "КОН - Na2SiO3". В качестве моделируемых показателей качества ТП были выбраны основные характеристики физико-механических свойств полученного покрытия детали: его микротвердость (Hm) и толщина (h). Моделируемыми технологическими параметрами были выбраны режимы МДО: плотность тока (Dt) и состав электролита, т.е. концентрации содержания в нем жидкого стекла Na2SiO3 и едкого калия КОН (CNa2SiO3 и CKOH соответственно).
При построении полиномиальных моделей получено, что истинную зависимость выбранных показателей качества ТП от режимов МДО адекватно отражают квадратичные полиномы. Обработка и анализ результатов натурных экспериментов, построение аналитических зависимостей, а также их графическая визуализация осуществлялись с помощью математического пакета MATCHCAD.
В отличие от классических статистических моделей нейросетевой аппарат можно использовать не только для моделирования вышеуказанных зависимостей (в данном случае в виде численных алгоритмов). С использованием ИНС можно решить следующую задачу: определить управляющее воздействие (оптимизировать режимы), которое необходимо установить для получения в процессе обработки детали требуемых значений параметров, характеризующих ее физико-механические свойства.
В первом случае входной слой нейронов соответствует режимам (Dt, CKOH, CNa2SiO3), выходной слой - характеристикам результата ТП (Hm и h). Результат моделирования - двухслойный персептрон. Во втором случае входы ИНС соответствуют требуемым Hm и h, выходы - необходимым Dt, CKOH, CNa2SiO3. Результат моделирования - трехслойный персептрон. Построение и обучение ИНС проводилось в системе Neural Connection.
Построенные ММ сравнивались по критерию точности: были рассчитаны экспериментальные ошибки
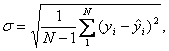(5)
где N - число экспериментов, yi - измеренная величина каждого отклика, 
- соответствующая величина, предсказанная с помощью ММ.
Показано, что ИНС проявляют более высокую точность, чем полиномиальные зависимости. Уменьшение s при переходе от полиномиальной к нейросетевой модели для Hm и h составляет соответственно 73 - 86% и 19 - 37% (в зависимости от выбранного алюминиевого сплава).
Была проведена серия проверочных натурных экспериментов. Получено, что расхождение данных ММ с результатами эксперимента не превышает 6%. Отметим, что нейронные сети и в этом случае дают более точный прогноз по сравнению с полиномиальной моделью.
На основе построенных ММ были разработаны компьютерные программы для проведения имитационных экспериментов. Программные средства реализованы в среде Visual Basic в удобном для пользователя интерфейсе.
Была разработана модифицированная схема управления ТП восстановления и упрочнения деталей МДО, включающая блок проведения компьютерных экспериментов.
Разработанные ММ и компьютерные программы являются универсальными, их можно внедрять для управления различными ТП, которые используются при ремонтно - восстановительных работах автотранспортной и сельскохозяйственной техники в целях повышения качества конечной продукции, экологичности производственных процессов, снижения потребления природных и материальных ресурсов.
С ПИСОК ЛИТЕРАТУРЫ
- Вознесенский В.А. Статистические методы планирования эксперимента в технико-экономических исследованиях. - 2-е изд. перераб. и доп.- М. Финансы и статистика. 1981.-263 С.
- Круглов В.В., Борисов В.В. Искусственные нейронные сети. Теория и практика.- М.: Горячая линия - Телеком. 2001. -382 С.
- Короткий С. Нейронные сети: алгоритм обратного распространения //http: //www. neuropower. de /rus/ books/ index. html.