Особое место среди таких моделей занимает полиномиальная система класса вычетов (ПСКВ), с помощью которых возможна организация ортогональных преобразований сигналов в расширенных полях Галуа GF(pv) [1,2]. Основным достоинством системы класса вычетов является сравнительная простота выполнения модульных операций (сложения, вычитания, умножения). Формальные правила выполнения таких операций в ПСКВ позволяют существенно повысить скорость вычислительных устройств ЦОС.
Одной из немодульных процедур, выполняемой спецпроцессором (СП) класса вычетов, является реализация прямого преобразования кода позиционной системы счисления (ПСС) в код ПСКВ. В настоящее время нашли широкое применение несколько методов перевода из ПСС в ПСКВ. Один из основополагающих методов перевода является метод понижения разрядности числа [1,3]
. (1)
Таким образом, для получения требуемого вычета 
предлагается использовать повторение вычислительной модели
, где 
, (2)
При этом для реализации (2) используется позиционный сумматор.
Однако реализация выражения (2) характеризуется необходимостью проверки условий окончания процесса итераций по контролю знака полученной разницы в операции вычитания, что значительно снижает быстродействие системы. А при достаточно большой размерности входных данных количество итераций может быть достаточно большим, что снижает быстродействие системы в целом.
Устранить указанные недостатки можно отказавшись от обратных связей в нейронных сетях (НС) конечного кольца, реализовав обработку на сети прямого распространения [1]. Число слоев в такой сети определяется количеством итераций l, необходимых для преобразования входных данных, а количество нейронов в каждом слое - разрядностью обрабатываемых данных на каждой из итераций. Веса, связывающие i -й нейрон с j -м нейроном следующего слоя, определяются 
. Тогда итеративный алгоритм преобразования A по модулю p определяется выражением
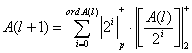, (3)
Замена обратных связей в НС на прямые позволяет повысить скорость обработки данных, так как в такой сети одновременно обрабатывается несколько отсчетов и в каждом такте работы сети на входе формируются преобразованные данные.
Повысить скорость реализации прямого преобразования из кода ПСС в код ПСКВ можно за счет метода непосредственного суммирования [1,3]. Преобразование исходного A(z), заданного в поле GF(pv), в полиномиальную систему класса вычетов осуществляется с помощью набора констант, являющихся эквивалентами степеней оснований 2i и коэффициентов при соответствующих степенях оснований ai(z), представленных в ПСКВ
, 
. (4)
Для получения значений A(z) в системе класса вычетов с основаниями 
необходимо получить в этой системе значения 
. В этом случае остаток по модулю pi(z) определяется
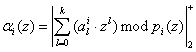, (5)
где 
, i=1,2,3,...,n.
В соответствии с (5), перевод A(z) из ПСС в непозиционную можно свести к суммированию по модулю два величин 
в соответствии с заданным полиномом A(z).
Пример. Определить остаток 
по модулю 
.
Для перевода из ПСС в ПСКВ воспользуемся выражением (5). Тогда значения остатков степеней оснований и коэффициентов при них равны
Тогда, согласно (5), получаем
.
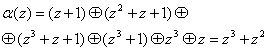Таким образом,
.
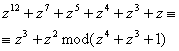В работе [1] представлена матрица связанности, т. е. синаптические веса нейронной сети, представляются в виде матрицы, строки которой соответствуют области аксонов предыдущего слоя, а столбцы - рецепторным полям нейронов последующего слоя. Разрабатываемая НС для перевода из ПСС в ПСКВ содержит 2 слоя. Первый слой состоит из 15 нейронов, на входы которых подается исходный полином в двоичном коде. С выходов нейронов первого слоя сигналы поступают на входы нейронов 2-го слоя в соответствии с матрицей T12
При этом операция перевода осуществляется всего за одну итерацию, что является существенным преимуществом по сравнению с ранее рассмотренными методами перевода. Структура НС, реализующей перевод по p(z) = z4+z3+1 в ПСКВ поля GF(24), представлена [1].
Таким образом, очевидно, что реализация метода непосредственного суммирования для полиномиальной системы класса вычетов позволяет разрабатывать высокоскоростные преобразователи кодов для вычислительных структур реального масштаба времени.
СПИСОК ЛИТЕРАТУРЫ
- Элементы компьютерной математики и нейроноинформатики /Червяков Н.И., Калмыков И.А., Галкина В.А., Щелкунова Ю.О., Шилов А.А.. - М.: ФИЗМАТЛИТ, 2003. - 216 с.
- Червяков Н.И., Калмыков И.А., Щелкунова Ю.О., Бережной В.В. Математическая модель нейронных сетей для исследования ортогональных преобразований сигналов в расширенных полях Галуа. - Нейрокомпьютеры: разработка и применение. 2003, №6, с.61-68.
- Калмыков И.А. Математические модели нейросетевых отказоустойчивых вычислительных средств, функционирующих в полиномиальной системе классов вычетов/Под ред. Н.И. Червякова. - М.: ФИЗМАТЛИТ, 2005. - 276 с.