; (1)
, (2)
где 
- поворачивающий коэффициент;x(n) - количество отсчетов,
,
.
Известно, что реализация прямого и обратного ДПФ предопределяет значительные погрешности при вычислении значений спектральных коэффициентов в поле комплексных чисел. С этой точки зрения наиболее привлекательными являются преобразования, определенные над расширенным полем Галуа 
. Пусть β является элементом порядка k в мультипликативной группе ненулевых элементов . Тогда выражение (1) имеет вид
,
. (3)
Преобразование обратное (3), определяется выражением
,
, (4)
где d* - целое число, удовлетворяющее условию
. (5)
Анализ выражений (3) и (4) показывает, что полученное преобразование аналогично ДПФ комплексной области и действует в пространстве циклической группы порядка d, определенной полем GF (pv). Так как βkn и x(n) представляют собой целочисленные элементы расширенного поля Галуа, то при реализации выражений (3) и (4) будут полностью отсутствовать шумы округления. Поэтому оценка спектральных составляющих с помощью (3) и (4) будет более точной по сравнению с ДПФ.
Пусть дана последовательность 
. Представим её в двоичном виде 
. Исходя из условия возможности представления квантованных значений x(n) в виде элементов расширенного поля Галуа , получаем входной вектор 
.
Преобразуем выражение (3) к матричному виду. Тогда значения спектральных составляющих можно представить
(6)
Следует отметить, что операции сложения при вычислении выходного вектора 
выполнялись по модулю 2, а операции умножения - по модулю порождающего полинома 
.
Для осуществления обратного преобразования необходимо воспользоваться выражением (4), предварительно определив значение обратного элемента d*. Согласно равенству (5) он равен единице, т.е. d* =1 . Тогда выражение (4) в матричной форме примет следующий вид:
(7)
Для повышения эффективности реализации задач ЦОС целесообразно обработку одномерных сигналов свести к обработке многомерных сигналов [1,3]. Отправной точкой при решении данной проблемы является изоморфизм, порожденный теоремой теории чисел, называемой китайской теоремой об остатках (КТО). Согласно данной теореме, если 
и pi- простые числа, то кольцо Zp класса вычетов по модулю P изоморфно прямой сумме
конечных полей GF (pi):
. (8)
Основным преимуществом - арифметики является возможность организации параллельных вычислений и, следовательно, значительное повышение быстродействия арифметических устройств.
Если в качестве оснований новой алгебраической системы выбрать минимальные многочлены pi(z) поля GF(pv), то любой полином A(z), удовлетворяющий условию
A(z) € P пол
где
, (9)
можно представить в виде n-мерного вектора
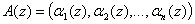, (10)
где 
, i = 1,2,...,n.
Так как сравнения по одному и тому же модулю можно почленно складывать, вычитать и умножать [2], то для суммы, разности и произведения A(z) и B(z), имеющих соответственно модулярные коды 
и 
справедливо:
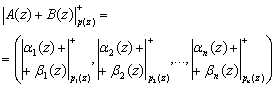,(11)
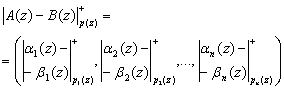,(12)
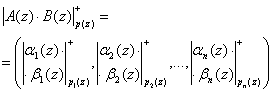. (13)
Таким образом, выполнение операций над операндами в GF(pv) производятся независимо по каждому из модулей pi(z), что указывает на параллелизм данной алгебраической системы.
Рассмотрим пример. Пусть задано расширенное поле Галуа GF (23) . Для данного поля определены минимальные многочлены
;
;
.
Найдем сумму и произведение двух полиномов 
и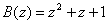 
. Данные полиномы принадлежит диапазону P(z), который определяется следующим выражением:
Представим исходные полиномы в виде модулярного кода по основаниям p1(z),p2(z) ,p3(z) . Тогда 
, а 
.
Сумма двух полиномов в GF(23) равна
.
Реализуем данную операцию, используя выражение (11).
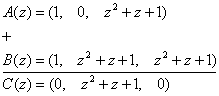
Следует отметить, что операции сложения и вычитания в расширенных полях Галуа GF(pv) выполняются по модулю p, то есть в рассмотренном примере по модулю 2.
Выполним операцию умножения данных полиномов
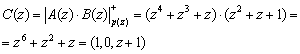
Реализуем данную операцию, воспользовавшись выражением (13). Тогда
,
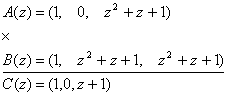где 
Из приведенного примера видно, что выполнение операции сложения и умножения в полиномиальном виде и в виде кода ПСКВ дает один и тот же результат. При этом порядок операндов A(z) и B(z) был уменьшен более чем в 2 раза, что является базовой предпосылкой для построения высокоскоростных вычислительных устройств ЦОС.
Таким образом, применение полиномиальной системы классов вычетов позволяет осуществлять ортогональные преобразования сигналов с использованием параллельных вычислений.
СПИСОК ЛИТЕРАТУРЫ
- Калмыков И.А. Математические модели нейросетевых отказоустойчивых вычислительных средств, функционирующих в полиномиальной системе классов вычетов/Под ред. Н.И. Червякова. - М.: ФИЗМАТЛИТ, 2005. - 276 с
- Калмыков И.А., Чипига А.Ф. Структура нейронной сети для реализации цифровой обработки сигналов повышенной разрядности/Вестник Ставропольского Государственного Университета,2004, Выпуск №38 с.46-50.
- Элементы применения компьютерной математики и нейроинформатики/Н.И. Червяков, И.А. Калмыков И.А., В.А. Галкина, Ю.О. Щелкунова, А.А. Шилов; Под ред. Н.И. Червякова. - М.: ФИЗМАТЛИТ, 2003. - 216с.