Уравнения движения намагничивающихся жидкостей в пористых средах имеют вид [1]:
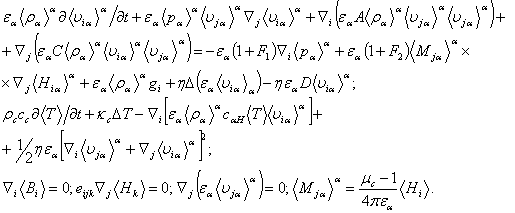(1)
Здесь εα- пористость матрицы; A, С, D, F1 и F2 - скаляры, характеризующие свойства среды; индексом a обозначены величины, относящиеся к жидкости; угловые скобки с индексом a означают локальное объемное усреднение по фазе a [2, З], а без индекса a - объемное усреднение по смеси (матрица + жидкость);ρc ,cc ,κc ,μc - плотность, теплоемкость, коэффициент теплопроводности и магнитная проницаемость смеси [1]; остальные обозначения общепринятые.
Усредненное по смеси магнитное поле и индукция 
находятся из усредненных по смеси уравнений Максвелла. Усредненная по объему, занятому жидкостью, намагниченность выражается через . Магнитная проницаемость смеси μc предполагается известной функцией от εα,<ρα>α , , .
Перейдем к определению усредненного по объему, занятому жидкостью, поля α>α, входящего в первое уравнение (1).
Усредняя по фазе α уравнение 
, будем иметь:
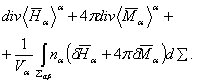(2)
Здесь Vα - объем усреднения, занятый жидкостью; ∑αβ - поверхность раздела фаз α и β (индекс β относится к матрице) в объеме усреднения V;n¯α - нормаль к ∑αβ, внешняя для фазы α; 
.
Поверхностный интеграл в формуле (2) отличен от нуля только в том случае, когда 
и 
т.е. когда векторные поля 
и 
, а следовательно, и 
и 
неоднородны в пространстве. Таким образом, поверхностный интеграл должен быть функцией от 
, обращающейся в нуль вместе с аргументом.
Разлагая эту функцию в ряд, будем иметь:
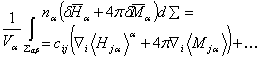
Предполагая функции 
и 
медленно изменяющимися в объеме усреднения, будем отбрасывать все малые высших порядков в разложении. В случае изотропной пористой среды тензор cij должен быть изотропным. Единственным изотропным тензором второго ранга является произведение скаляра на единичный тензор δij [4]. С учетом этого обстоятельства уравнение (2) принимает вид%
(3)
Усредняя по фазе α уравнение 
, будем иметь:
(4)
Здесь eijk - тензор Леви-Чивита.
Разлагая в формуле (4) поверхностный интеграл в ряд, аналогично находим:
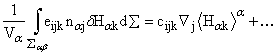
Здесь тензор cijk также должен быть изотропным. Как известно [4], cijk должен в этом случае равняться произведению скаляра на тензор eijk. Тогда формула (4) принимает вид 
. Отметим, что, когда поле сильно изменяется в объеме усреднения, например вблизи проводников с током, проходящих в пористой среде, необходимо учитывать и следующие члены разложения.
Вводя потенциал поля по формуле 
, уравнение (3) можно записать в виде:
Общее решение этого уравнения имеет вид:
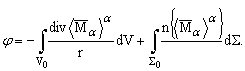
Здесь 
;n¯ - внешняя нормаль к объему V0, занятому пористой средой; ∑0 - поверхность этого объема; индекс 1 относится к пористой среде, 2 - к окружающему объему.
Отметим, что в случае, когда пористость матрицы мала, нахождение поля существенно упрощается; тогда имеет место формула [1]:
(5)
Если среда находится в состоянии магнитного насыщения, а внешнее приложенное поле H¯0 достаточно велико, можно принять 
. Далее, при выводе уравнений конвекции, ограничимся этим наиболее важным для практики случаем. Вводя скорость фильтрации 
, коэффициент проницаемости 
[5], опуская для краткости угловые скобки и ограничиваясь случаем медленных фильтрационных течений, уравнения системы (1) запишем в виде:
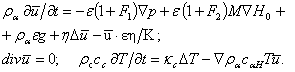(6)
Во втором уравнении (6) пренебрегается вязкой диссипацией и магнитокалорическим эффектом. Отметим также, что слагаемое 
в первом уравнении (6), соответствующее модели фильтрации Бринкмана [5], в случае медленных фильтрационных течений мало.
Применяя к системе (6) известную процедуру вывода уравнений конвекции [6, 7], будем иметь:
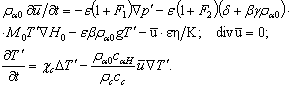(7)
Здесь 
;
;
;
; индексом нуль обозначены постоянные средние значения величин в состоянии механического равновесия, штрихом - отклонения от равновесия.
Далее ограничимся для определенности случаем, когда заданный градиент магнитного поля 
вертикален (k¯ - единичный вектор оси z, направленной вверх). Взяв rot от обеих частей уравнения равновесия (7), когда u¯=0, с учетом уравнения теплопроводности находим, что, как и в обычной гидродинамике [б], необходимое условие равновесия имеет вид 
, где A = const.
Запишем уравнения (7) в безразмерном виде:
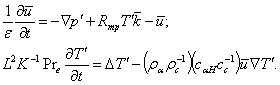
Здесь приняты следующие единицы измерения: длины - L - характерный размер задачи; скорости - 
; времени - 
, температуры - AL; давления - 
;
;
эффективное число Прандтля;Rmp - число Рэлея, имеющее вид
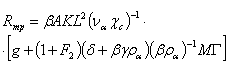
Отметим, что отсутствие в уравнениях фильтрации, приведенных в монографии [6], скаляров, аналогичных скалярам F1 и F2 , связано с отбрасыванием поверхностных интегралов по межфазной поверхности ∑αβ в процессе усреднения уравнений гидродинамики.
СПИСОК ЛИТЕРАТУРЫ
- Тактаров Н.Г. Движение намагничивающихся жидкостей в пористых средах //Магнитная гидродинамика. - 1980. - № 3. - С. 38 - 4 2.
- Gray W. G. A derivation of the equations for multi-phase transport. - Chem. Eng. Sci., 1975, vol. 30, p. 229 - 233.
- Gray W. G., O´Neill K. On the general equations for flow in porous media and their reduction to Darcy´s law. - Water Resources Research, 1976, vol. 12, N 2, p. 148 - 154.
- Джеффрис Г., Свирлс Б. Методы математической физики. Т. 1. М.: Мир, 1969. - 124 с.
- Коллинз Р. Течения жидкостей через пористые материалы. М.: Мир, 1964. - 352 с.
- Гершуни Г. 3., Жуховицкий Е. М. Конвективная устойчивость несжимаемой жидкости. М.: Наука, 1972. 392 с.
- Lalas D. P., Carmi S. Thermoconvective stability of ferrofluids. - Phys. Fluids, 1971, vol. 14, N 2.