Scientific journal

Modern high technologies

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

Наиболее распространёнными моделями описания заряда и потенциала пылевой частицы в плазме является модель ограниченных орбит (ОО), модель радиального дрейфа (РД) и гидродинамическая модель диффузионного ограничения (ДО) [1].

Модель ОО, перенесённая из теории зондов, предполагает беcстолкновительное движение ионов в поле частицы из бесконечности с сохранением полной энергии и момента количества движения, при отсутствии потенциальных барьеров на всём пути:

.

Плотности электронного и ионного токов, согласно модели ограниченных орбит, равны:

,                     (1)

.                  (2)

Здесь n_e∞, n_i∞, T_e, T_i, m, M - концентрации, температуры и массы электронов и ионов на бесконечности, φ_а - потенциал частицы, θ - угол между радиус-вектором и направлением скорости. Равенство этих токов в стационарном случае определяет заряд и потенциал частицы.

В последнее время к применимости модели ОО высказан ряд сомнений. В [2] показано, что потенциальные барьеры при максвелловском распределении на бесконечности возникают всегда, даже при малых радиусах частицы. В [3-4] указывается, что даже редкие ион-атомные столкновения существенно влияют на ионный ток, разрушая орбитальное движение ионов. Ещё большее влияние при низких давлениях должна оказывать ионизация в объёме, так как ионный ток на частицу должен полностью компенсироваться ионизацией в объёме ячейки межчастичной области. Следовательно, фактическая длина пробега ионов составляет меньше половины межчастичного расстояния. Разрушение орбитального движения ионов, особенно при низкой ионной температуре, является предпосылкой применимости модели радиального дрейфа [5]. В этой модели ионный ток на частицу формируется на бесконечности и постоянен до самой частицы. Ионы двигаются чисто радиально со скоростями, определяемыми локальным потенциалом и законом сохранения энергии (MV²_r=2eφ(r)). Следовательно, уравнение Пуассона будет иметь вид:

_.                              (3)

Отметим, что для скорости ионов радиальная модель является частным случаем гидродинамического приближения, справедливого при большой частоте столкновений ион-нейтрал ν_im.

,                  (4)

Более того, в гидродинамическом приближении введение в уравнение непрерывности ионизационного члена позволяет рассматривать процесс формирования ионного потока , где z - количество ионизаций на один электрон в единицу времени. При высоких давлениях необходимо вводить и рекомбинационный член [6]. При низких давлениях роль частоты столкновений в уравнении движения (4) выполняет частота ионизации, аналогичным образом тормозящая поток ионов, так как образовавшийся в результате ионизации, ион не имеет начальной скорости.

В настоящей работе рассмотрено формирование ионного потока на частицу за счёт ионизации в межчастичной области в плазме низкого давления как в режиме свободного пролёта ионов, так и в гидродинамическом приближении.

Будем рассматривать пылевую частицу радиусом «a», окружённую сферической ячейкой Зейтца-Вигнера с радиусом r_d, определяемым концентрацией частиц r_d=(4/3πn_d)^-1/3. Внешний поток заряженных частиц на ячейку отсутствует виду полного окружения частицы другими частицами. Внутри ячейки формируется ионный поток за счёт ионизации газа электронами:

                (5).

Это уравнение непрерывности в дифференциальной форме имеет вид:

.

Концентрацию ионов можно получить, как и в работе Тонкса-Ленгмюра [7], учитывая индивидуальную скорость образовавшихся ионов

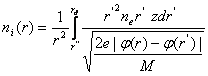 .                   (6).

Концентрацию электронов будем предполагать распределённой по Больцману:

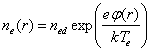 ,                   (7).

где n_ed - концентрация электронов на границе ячейки.

Тогда уравнение Пуассона запишется в виде

          (8)

На границе ячейки ввиду подобности соседних ячеек положим нулевое значение потенциала и его градиента. Потенциал на поверхности частицы определяется в процессе решения подбором частоты ионизации z^, с тем, чтобы ионный ток на частицу по (5) сравнивался с электронным, определяемым согласно (1).

Аналогичное уравнение «плазма-слой» выведено Ленгмюром [7] для положительного столба газового разряда. Однако граничные условия у Ленгмюра были обратные: нулевое значение потенциала и его градиента в центре плазмы и автоматически устанавливающийся потенциал внешней стенки. Численное решение уравнения затруднено из-за неопределенности правой части при близком к нулю значении знаменателя. Часто всю область возмущения разбивают на две подобласти: подобласть квазинейтральной плазмы с нулевой левой частью уравнения и подобласть слоя, где пренебрегается концентрацией электронов и поток ионов считается постоянным. В нашем случае, когда размер слоя сравним с размерами всей ячейки, такое приближение неприменимо. Введём безразмерные величины

, , ,

, ,

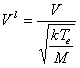где ω_i - ионная плазменная частота. Тогда уравнение (8) будет иметь вид

,                    (8´)

где выражения для концентрации электронов и ионов будут следующими:

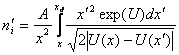, .     (9)

Численное решение начнём от границы ячейки, где для начального тонкого слоя Δx<<x_d , считая задачу плоской, можно получить аналитическое решение. Положим n´_e=1, а n´_i=const≥1. Тогда уравнение (8´) интегрируется просто

, , .                 (10)

Здесь x отсчитываем от границы ячейки. Подставив полученное решение в выражение для концентрации ионов получим:

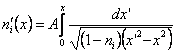, или

.

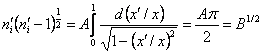Корень кубического уравнения n´_i²(n´_i-1)=B определяется выражением

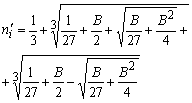                (11).

Таким образом, задавая параметр А, можно рассчитать начальную концентрацию ионов и начальный ход потенциала.

Для большей устойчивости численного решения использовались параболическая интерполяция потенциала по трём точкам:

,

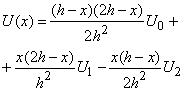где h - шаг дискретизации, x - отсчитывается от точки x₀ ,а также приближённое аналитическое решение для концентрации на каждом шаге:

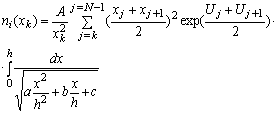,(12),

где a=U_j-2U_j+1+U_j+2, b=-3 U_j+4 U_j+1- U_j+2, c=2 U_j-2U_k, причём

.

Такое приближение хорошо согласуется с аналитическим решением внешнего слоя (10).

Параметр A, пропорциональный частоте ионизации, определяется радиусом частицы так, чтобы формируемый ионный ток (5) сравнялся с электронным током

.

В безразмерном виде это условие запишется:

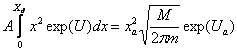.              (13).

Для устранения подбора задавались значения x_d и А. Радиус частицы x_a определялся в процессе счёта при выполнении условия (13).

Результаты численных расчётов приведены на рисунке 1 и в таблице 1.

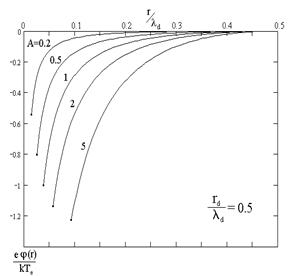
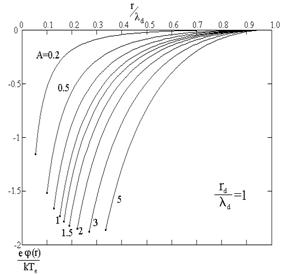
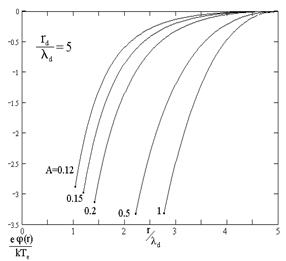
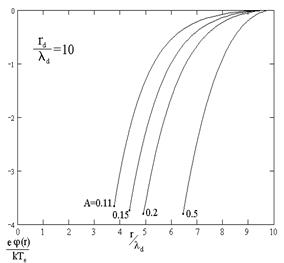
Рисунок 1. Результаты численных расчётов

Окончания кривых на графиках определяют радиус и потенциал пылевой частицы.

Ход потенциала вблизи границы ячейки во всех случаях определяется зависимостью

.

Вблизи частицы он близок к экспоненте. Заряд частицы, определённый по градиенту потенциала на её поверхности, соответствует разности полных зарядов ионов и электронов в ячейке. Это подтверждает правильность решения уравнения Пуассона. В то же время сам потенциал частицы менее отрицателен, чем потенциал изолированной частицы с тем же зарядом, но без плазмы, за счёт большего вклада ионной компоненты плазмы. Из-за неравномерности и неодинаковости распределения электронов и ионов по ячейке разность концентраций электронов и ионов на границе ячейки не равна концентрации частиц умноженной на их заряд.

В таблице 2 приведены результаты численного расчёта распределения потенциала и заряда в ячейке Зейтца-Вигнера в гидродинамическом приближении с учётом ионизации в объёме. В этом приближении индивидуальные скорости ионов заменяются усреднёнными по ансамблю. Уравнение движения ионов запишется

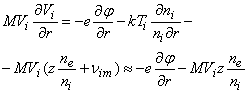           (14).

Пренебрегая градиентом давления и столкновениями ионов с атомами и интегрируя, получим

.

В безразмерных переменных будем иметь

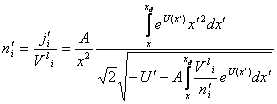 (15).

Несмотря на то, что n_i в (15) определяется через неизвестное n_i в правой части, задача решается с помощью итераций. Аналитическое решение вблизи границы ячейки изменяется незначительно. Полагая n´_e=1, а n´_i=const≥1 в плоском приближении получаем

, .

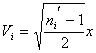Для концентрации n_i получаем уравнение

.

Таблица 1. Результаты численных расчётов

Таблица 2. Результаты численных расчётов

Здесь  вместо имевшегося ранее соотношения для свободнопролётного случая , что слабо влияет на значение концентрации ионов. Сравнение таблиц 2 и 1 указывает на весьма близкие значения полученных данных. Это позволяет использовать гидродинамическое приближение не только при высоких давлениях, но и при промежуточных и даже низких давлениях.

Исследования, описанные в данной работе, были проведены в рамках проекта PZ-013-02, поддерживаемого совместно Американским фондом гражданских исследований и развития (АФГИР), Министерством образования РФ и правительством Республики Карелия.

СПИСОК ЛИТЕРАТУРЫ

1. Цытович В.Н., Морфилл Г.Е., Томас В.Х. Физика плазмы. 2002. т.28. №8. с.675-707.
2. Allen J.E., Annaratone B.M., U. de Angeles J. Plasma Phisics. V.63. 2000. p.299.
3. Швейгерт В.А., Швейгерт И.В., Богданов В.М. и др. ЖЭТФ. Т.115. 1999. с.877.
4. Зобнин А.В., Нефёдов А.П., Синельников В.А., Фортов В.Е.ЖЭТФ. т.118. вып.3(9) 2000 с. 554-559.
5. Nairn C.M.C., Annaratone B.M., Allen J.E. Plasma Sources Sci. Technol. V.7. 1998. p.478.
6. Паль А.Ф., Старостин А.Н., Филиппов А.В. Физика плазмы. Т.27. 2001. №2. с.155-164. т.28. 2002. №1. с.32-44.
7. Tonks L., Langmnuir I. Phisycal Review. 1929. v.34. p.876-922.