![]() (1)
(1)
В [1] было показано, что закон распределения ФВМ зависит от параметра b функции и не зависит от фрактальной размерности D. Поэтому при моделировании микроускорений с помощью ФВМ можно использовать условие равенства нулю фазы ФВМ, а необходимый закон распределения выбирать, исходя из значений параметра b.
В данной работе рассматривается значение b = 0,2. Результаты проверки нормальности закона распределения ФВМ с помощью критерия согласия χ2-Пирсона представлены на рис. 1-3.
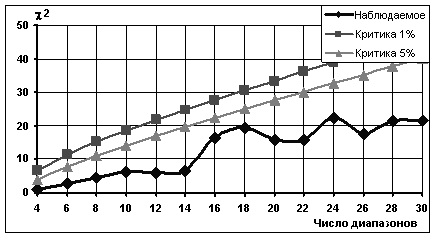
Рисунок 1. Изменение критерия согласия для ФВМ b = 0,2; D = 1,993
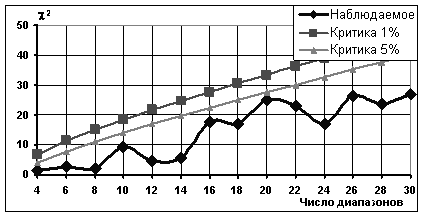
Рисунок 2. Изменение критерия согласия для ФВМ b = 0,2; D = 1,997
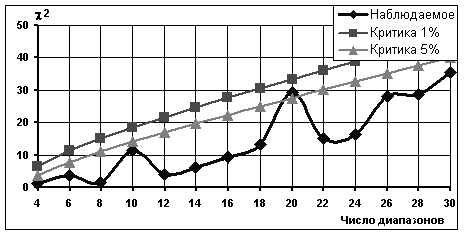
Рисунок 3. Изменение критерия согласия для ФВМ b = 0,2; D = 1,9[20]
Как видно из приведенных зависимостей, нормальный закон распределения проходит для всех исследуемых точек, кроме одной (20 диапазонов при D = 1,9,[20], где цифра в квадратных скобках обозначает число девяток после запятой). Да и в последнем случае гипотеза нарушается на 5%-м уровне значимости и проходит на 1%-м. Однако кривая наблюдаемого значения χ2-Пирсона постепенно приближается к критическим прямым. При b = 0,1 гипотеза не может быть с уверенностью принята даже на 1%-м уровне (рис. 4-5). Это означает, что нужный коридор значений параметра ФВМ располагается приблизительно в следующих пределах:0,15<b<0,45 . Следует провести его дальнейшее уточнение в будущем, исследовав ФВМ при граничных значениях . Однако нужно иметь в виду, что уточнение границ этого диапазона приводит к размыванию однозначности принятия или отвержения гипотезы о нормальном законе распределения.
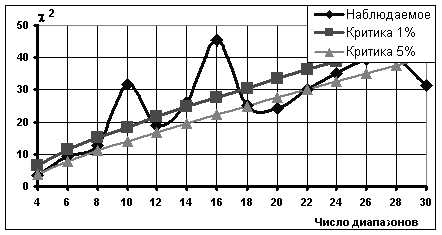
Рисунок 4. Изменение критерия согласия для ФВМ b = 0,1; D = 1,995
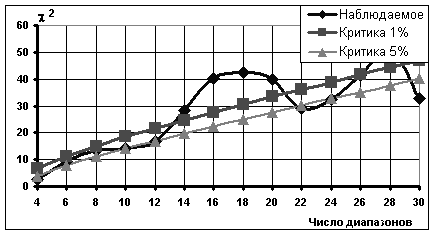
Рисунок 5. Изменение критерия согласия для ФВМ b = 0,1; D = 1,997
Гораздо больший интерес представляют собой исследования по выявлению тех законов распределения, в которые переходит нормальный закон при переходе за левую и правую границы обозначенного диапазона.
Нормальность закона распределения позволяет с помощью критериев однородности оценить и те коридоры значений параметров ФВМ, при которых она может считаться случайной величиной.
СПИСОК ЛИТЕРАТУРЫ
- Седельников А.В., Корунтяева С.С., Чернышева С.В. Проверка закона нормального распределения фрактальной функции Вейерштрасса-Мандельброта //Успехи современного естествознания. - 2005. - № 11. - с. 37-38.



