В данной работе для решеток ПК, ГЦК, ОЦК, используется метод построения кординационных сфер, рассмотренный в работах [1-3] и отличающийся от способа, принятого в кристаллографии введением сфер не занятых атомами, названных 0-сферами. В работах [1-3] устанавливается связь между этими нумерациями координационных сфер, приводится алгоритм нахождения координационных чисел, показывается, что расположение узлов на любой координационной сфере может быть представлено сочетанием вершин вложенных друг в друга семи многогранников. Связь между нумерацией координационных сфер для простой кубической, ОЦК и ГЦК решеток соответственно, представлена следующими уравнениями [3]:
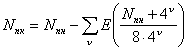
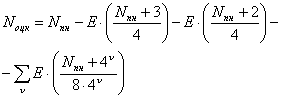
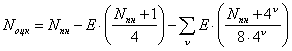
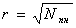- связь между радиусом и номером координационной сферы. Для построения координационных сфер различных материалов кубической симметрии была создана программа написанная на языке Delphi. Интерфейс программы приведен ниже. Программа позволяет построить координационную сферу, определить индексы плоскостей полученного многогранника и определить номер координационной сферы в соответствие с номером, определяемым традиционным методом в кристаллографии. Программа с успехом может быть использована не только в исследовательской работе, но и в курсе общей физики при изучении элементов кристаллографии.
Например, необходимо построить координационную сферу с порядковым номером 14 (см. интерфейс программы). В этом случае вводим в первом поле интерфейса номер 14, а в третьем поле параметр решетки. Нажимаем клавишу рассчитать. Во втором поле получаем значение номера координационной сферы, определяемый традиционными методами кристаллографии, значения координат атомов (узлов) заполняющих сферу, значение радиуса координационной сферы, общее число узлов и тип многогранника. В левом поле интерфейса происходит построение модели многогранника.
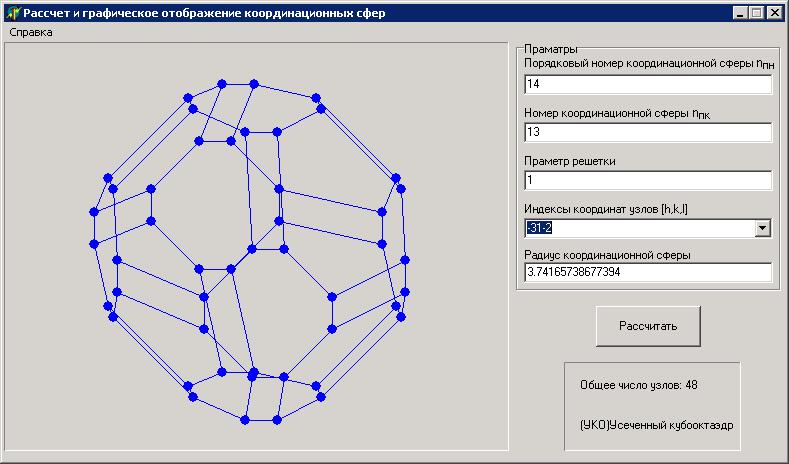
Рисунок 1. Интерфейс программы «Сферы».
Список литературы
- Старостенков М.Д. Пространственное распределение атомов по координационным сферам в кристаллах кубической симметрии //Кристаллография. 1992. Т.37. Вып.3. С.717-723.
- Старостенков М.Д., Дмитриев С.В. Распределение пространственных многогранников по координационным сферам в ОЦК-решетке //Журнал структурной химии.1993. Т.34. № 4. С. 107-111.
- Дмитриев С.В., Старостенков М.Д., Жданов А.Н. Основы кристаллогеометрического анализа дефектов в металлах и сплавах: Учебное пособие для вузов /Алт. гос. тех. ун-т им. И.И. Ползунова.-Барнаул:Изд-во АлтГТУ, 1995.-256 с.